2 Elementos de Modelos Probabilísticos em Grafos
2.1 Grafo Direcionado
Definição 2.1.
Um grafo direcionado, , é composto por um conjunto de vértices, , e e um conjunto de arestas, , onde cada aresta é um par ordenado de vértices, isto é, .
Para auxiliar nossa intuição sobre a Definição 2.1, é comum representarmos o grafo por meio de uma figura. Nesta, representamos cada vértice por meio de um ponto. Além disso, para cada aresta, , traçamos uma seta que aponta de para .
Por exemplo, considere que os vértices são e as arestas são . Neste caso, teremos os pontos como vértices e, além disso, traçaremos setas de para e para e, também, de para . Podemos desenhar este grafo utilizando os pacotes dagitty e ggdag (Barrett2022, Textor2016):
library(dagitty) library(ggdag) library(ggplot2) # Especificar o grafo grafo <- dagitty("dag { V1 -> { V2 V3 } V2 -> V3 }") # Exibir a figura do grafo ggdag(grafo, layout = "circle") + theme(axis.text.x = element˙blank(), axis.ticks.x = element˙blank(), axis.text.y = element˙blank(), axis.ticks.y = element˙blank()) + xlab() + ylab()
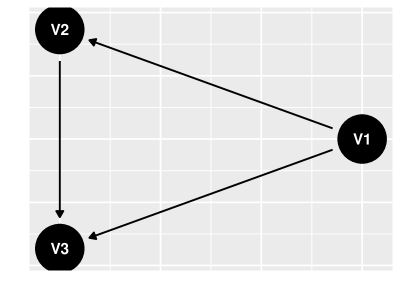
Grafos direcionados serão úteis para representar causalidade pois seus vértices serão variáveis e suas arestas irão apontar de cada causa imediata para seu efeito. Por exemplo, no Capítulo 1 consideramos um caso em que Sexo e Tratamento são causas imediatas de recuperação e, além disso, Sexo é causa imediata de Tratamento. O grafo na figur 1 poderia representar estas relações se definirmos que é Sexo, é Tratamento e é Recuperação.
Usando a representação de um grafo, podemos imaginar caminhos sobre ele. Um caminho direcionado inicia-se em um determinado vértice e, seguindo a direção das setas, vai de um vértice para outro. Por exemplo, é um caminho direcionado na figur 1, pois existe uma seta de para e de para . É comum denotarmos este caminho direcionado por . Similarmente, não é um caminho direcionado, pois não existe seta de para . A definição de caminho direcionado é formalizada a seguir:
Definição 2.2.
Um caminho direcionado é uma sequência de vértices em um grafo direcionado, tal que, para cada , .
Definição 2.3.
Dizemos que é descendente de se existe um caminho direcionado de em .
Um caminho é uma generalização de caminho direcionado. Em um caminho, começamos em um vértice e, seguindo por setas, mas não necessariamente na direção em que elas apontam, vamos de um vértice para outro. Por exemplo, na figur 1 vimos que não é um caminho direcionado pois não existe seta de para . Contudo, é um caminho pois existe uma seta ligando e , a seta que aponta de para . É comum representarmos este caminho por . Caminho é formalizado a seguir:
Definição 2.4.
Dizemos que vértices e são adjacentes se ou .
Definição 2.5.
Um caminho é uma sequência de vértices, tal que, para cada , e são adjacentes.
2.2 Grafo Direcionado Acíclico (DAG)
Um DAG é um grafo direcionado tal que, para todo vértice, , não é possível seguir setas partindo de e voltar para . Este conceito é formalizado a seguir:
Definição 2.6.
Um grafo direcionado acíclico (DAG) é um grafo direcionado, , tal que, para todo vértice, , não existe um caminho direcionado, tal que .
Usualmente representaremos as relações causais por meio de um DAG. Especificamente, existirá uma aresta de para para indicar que é causa imediata de . Caso um grafo direcionado não seja um DAG, então existe um caminho de em , isto é, seria uma causa de si mesma, o que desejamos evitar.
Um DAG induz uma ordem parcial entre os seus vértices. Isto é, se existe uma aresta de para , então podemos interpretar que antecede causalmente. Com base nesta ordem parcial, é possível construir diversas definições que nos serão úteis.
Dizemos que é pai de em um DAG, , se existe uma aresta de a , isto é, . Denotamos por o conjunto de todos os pais de . Similarmente é o conjunto de vértices que são pais de algum vértice em :
Definição 2.7.
O conjunto de pais de em um DAG, , é:
Similarmente, dizemos que é um ancestral de em um DAG, se antecede causalmente. Isto é, se é pai de ou, pai de pai de , ou pai de pai de pai de , e assim por diante Denotamos por o conjunto de todos os ancestrais de elementos de :
Definição 2.8.
Em um DAG, , o conjunto de ancestrais de , , é tal que e se e somente se existe e um caminho direcionado, C, tal que e .
Note que podemos interpretar como o conjunto de todas as causas diretas e indiretas de .
Finalmente, diremos que um conjunto de vértices, é ancestral em um DAG, se não existe algum vértice fora de que seja pai de algum vértice em . Segundo nossa interpretação causal, será ancestral quando nenhum vértice fora de é causa direta de algum vértice em :
Definição 2.9.
Dizemos que é ancestral em um DAG se, para todo vértice , temos que .
Lema 2.10.
Em um DAG, , para todo , é ancestral.
2.3 Modelo Probabilístico em um DAG
Um modelo probabilístico em um DAG é tal que cada um dos vértices é uma variável aleatória. O DAG será usado para descrever relações de independência condicional existentes entre estas variáveis. Mais especificamente, cada vértice será independente dos demais vértices dados os seus pais. Uma maneira alternativa de pensar sobre esta afirmação é imaginar que cada vértice é gerado somente pelos seus pais. Esta intuição é formalizada em Definição 2.11:
Definição 2.11.
Para um conjunto de variáveis aleatórias, dizemos que uma função de densidade sobre , , é compatível com um DAG, , se:
Quando não há ambiguidade, também dizemos que é compatível com neste caso.
Exemplo 2.12.
Considere que , e . Neste caso,
Como , decorre da Definição 2.11 que não é compatível com o DAG sem arestas em que . Em outras palavras, e não são independentes. Como sempre é verdade que e que , é compatível com os DAGs e com .
Exemplo 2.13.
Considere que . Isto é, são independentes segundo . Neste caso, é compatível com qualquer DAG sobre .
Quando tem muitos elementos, pode ser difícil verificar se a Definição 2.11 está satisfeita Para esses casos, pode ser útil aplicar o Lema 2.14:
Lema 2.14.
Uma função de densidade, , é compatível com um DAG, , se e somente se, existem funções, tais que:
Exemplo 2.15.
Considere que
Tome . Para , , e . Assim, tomando , e , temos que
Isto é, decorre do Lema 2.14 que é compatível com .
Exercício 2.16.
Usando a mesma do Exemplo 2.15, prove que é compatível com o DAG . Temos que é compatível com quais outros DAG’s?
Se é ancestral em um DAG, então pode ser decomposto de forma similar a . Este fato será útil e é formalizado no Lema 2.17.
Lema 2.17.
Seja um DAG. Se é ancestral e é compatível com , então
A seguir, estudaremos três tipos fundamentais de modelos probabilísticos em DAG’s com vértices. A intuição obtida a partir destes exemplos continuará valendo quando estudarmos grafos mais gerais.
2.4 Exemplos de Modelo Probabilístico em um DAG
Nos exemplos a seguir, considere que .
2.4.1 Confundidor (Confounder)
No modelo de confundidor, as únicas duas arestas são e . Uma ilustração de um confundidor pode ser encontrada na figur 2. O modelo de confundidor pode ser usado quando acreditamos que é uma causa comum a e a . Além disso, não é causa imediata de nem vice-versa.
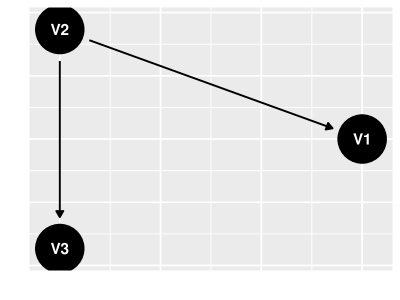
Em um modelo de confundidor a relação de dependência entre e é explicada pelos resultados a seguir:
Lema 2.18.
Para qualquer probabilidade compatível com o DAG na figur 2, .
Lema 2.19.
Existe ao menos uma probabilidade compatível com o DAG na figur 2 tal que .
Combinando os Lemas 2.18 e 2.19 é possível compreender melhor como usaremos confundidores num contexto causal. Nestes casos, será uma causa comum a e a . Esta causa comum torna e associados, ainda que nenhum seja causa direta ou indireta do outro.
Podemos contextualizar estas ideias em um caso de diagnóstico de dengue. Considere que é a indicadora de que um indivíduo tem dengue, e e são indicadoras de sintomas típicos de dengue, como dor atrás dos olhos e febre. Neste caso, e tipicamente são associados: caso um paciente tenha febre, aumenta a probabilidade de que tenha dengue e, portanto, aumenta a probabilidade de que tenha dor atrás dos olhos. Contudo, apesar dessa associação não tem influência causal sobre . Se aumentarmos a temperatura corporal do indivíduo, não aumentará a probabilidade de que ele tenha dor atrás dos olhos. A dengue que causa febre, não o contrário.
2.4.2 Cadeia (Chain)
No modelo de cadeia, as únicas duas arestas são e . Uma ilustração de uma cadeia pode ser encontrada na figur 3. Neste modelo, acreditamos que é causa de que, por sua vez, é causa de . Assim, é ancestral de , isto é, o primeiro é causa indireta do segundo.
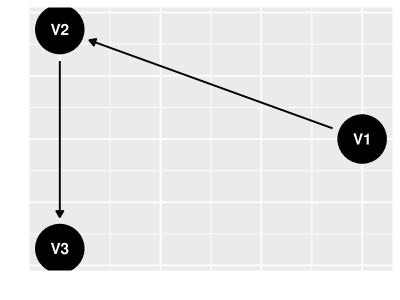
Em um modelo de cadeia a relação de dependência entre e é explicada pelos resultados a seguir:
Lema 2.20.
Para qualquer probabilidade compatível com o DAG na figur 3, .
Lema 2.21.
Existe ao menos uma probabilidade compatível com o DAG na figur 3 tal que .
Combinando os Lemas 2.20 e 2.21 é possível compreender melhor como usaremos cadeias num contexto causal. Nestes casos, será uma consequência de e uma causa de . Assim, a cadeia torna e e associados, ainda que nenhum seja causa direta do outro. Contudo, ao contrário do confundidor, neste caso é uma causa indireta de , isto é, tem influência causal sobre .
Para contextualizar estas ideias, considere que é a indicadora de consumo elevado de sal, é a indicadora de pressão alta, e é a indicadora de ocorrência de um derrame. Como consumo elevado de sal causa pressão alta e pressão alta tem influência causal sobre a ocorrência de um derrame, pressão alta é uma cadeia que é um mediador entre consumo elevado de sal e ocorrência de derrame. Assim, consumo elevado de sal tem influência causal sobre a ocorrência de derrame.
2.4.3 Colisor (Collider)
O último exemplo de DAG com vértices que estudaremos é o de modelo de colisor, em que as únicas duas arestas são e . Uma ilustração de um colisor pode ser encontrada na figur 4. O modelo de colisor pode ser usado quando acreditamos que e são causas comuns a . Além disso, não é causa imediata de nem vice-versa.
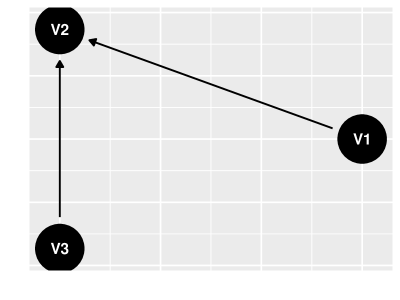
Em um modelo de colisor a relação de dependência entre e é explicada pelos resultados a seguir:
Lema 2.22.
Para qualquer probabilidade compatível com o DAG na figur 4, .
Lema 2.23.
Existe ao menos uma probabilidade compatível com o DAG na figur 4 tal que .
Combinando os Lemas 2.22 e 2.23 vemos como utilizaremos confundidores num contexto causal. Nestes casos, e serão causas comuns e independentes de . Uma vez que obtemos informação sobre o efeito comum, , e passam a ser associados.
Esse modelo pode ser contextualizado observando a prevalência de doenças em uma determinada população (Sackett1979). Considere que e são indicadoras de que um indivíduo tem doenças que ocorrem independentemente na população. Além disso, é a indicadora de que o indíviduo foi hospitalizado, isto é, é influeciado causalmente tanto por quanto por . Para facilitar as contas envolvidas, desenvolveremos o exemplo com distribuições fictícias. Considere que e são independentes e tem distribuição Bernoulli(0.05). Além disso, quanto maior o número de doenças, maior a probabilidade de o indíviduo ser hospitalizado. Por exemplo, , , , e .
Com base nestas especificações, podemos verificar se e estão associados quando . Para tal, primeiramente calcularemos algumas probabilidades conjuntas que serão úteis:
| (1) |
Com base nestes cálculos é possível obter a prevalência da doença dentre os indivíduos hospitalizados:
Finalmente,
Como , verificamos que não é independente de dado . De fato, ao observar que um indivíduo está hospitalizado e tem uma das doenças, a probabilidade de que ele tenha a outra doença é inferior àquela obtida se soubéssemos apenas que o indivíduo está hospitalizado.
Esta observação não implica que uma doença tenha influência causal sobre a outra. Note que a frequência de hospitalização aumenta drasticamente quando um indivíduo tem ao menos uma das doenças. Além disso, cada uma das doenças é relativamente rara na população geral. Assim, dentre os indíviduos hospitalizados, a frequência daqueles que tem somente uma das doenças é maior do que seria caso as doenças não estivessem associadas. Quando fixamos o valor de uma consequência comum (hospitalização), as causas (doenças) passam a ser associadas. Esta associação não significa que infectar um indivíduo com uma das doenças reduz a probabilidade que ele tenha a outra.
2.5 Modelo Causal (Causal Model)
Com base nos conceitos abordados anteriormente, finalmente podemos definir o Modelo Causal (CM ):
Definição 2.24.
Um CM é um par tal que é um DAG (Definição 2.6) e é uma função de densidade sobre compatível com (Definição 2.11). Neste caso, é comum chamarmos de grafo causal do CM .
Note pela Definição 2.24 que um CM é formalmente um modelo probabilístico em um DAG. O principal atributo de um CM que o diferencia de um modelo probabilístico genérico em um DAG é como o interpretamos. Existe uma aresta de em em um CM se e somente se é uma causa direta de .
Dentre os modelos causais, é de particular interesse o modelo linear Gaussiano.
Definição 2.25.
Dizemos que é um CM linear Gaussiano de parâmetros e se, existe matriz diagonal positiva, , , e tal que, para todo vértice , quando e
O modelo causal linear Gaussiano tem algumas propriedades especiais, que tornam mais simples suas compreensão. Algumas destas são apresentadas abaixo:
Lema 2.26.
Se é um CM linear Gaussiano, então segue distribuição normal multivariada.
Lema 2.27.
Seja um CM linear Gaussiano com coeficientes . Para cada , defina como o conjunto de todos os caminhos direcionados de a .
No próximo capítulo estudaremos consequências desta interpretação causal. Contudo, antes disso, a próxima seção desenvolverá um resultado fundamental de modelos probabilísticos em DAGs que será fundamental nos capítulos posteriores.
2.6 Exercícios
Exercício 2.28.
Em um DAG, , Considere que é definido como o menor conjunto tal que e, se , então . Prove que .
Exercício 2.29.
Prove o Lema 2.10.
Exercício 2.30.
Prove que se é ancestral, então .
Exercício 2.31.
Sejam e grafos tais que . Prove que se é compatível com , então é compatível com .
Exercício 2.32.
Prove o Lema 2.14.
Exercício 2.33.
Prove o Lema 2.17.
Exercício 2.34.
Prove que, para qualquer , .
Exercício 2.35.
Prove que é ancestral se e somente se .
Exercício 2.36.
Considere que são independentes e tais que . Além disso, .
-
(a)
Desenhe um DAG compatível com as relações de independência dadas pelo enunciado.
-
(b)
Prove que e são independentes. Isso contradiz sua resposta para o item anterior?
Exercício 2.37.
Para cada um dos modelos de confundidor, cadeia e colisor, dê exemplos de situações práticas em que este modelo é razoável.
Exercício 2.38.
Considere que, dado , são i.i.d. e . Além disso, .
-
(a)
Seja dada pelo enunciado. Exiba um DAG, , tal que é compatível com .
-
(b)
são independentes?
-
(c)
Determine .
Exercício 2.39.
Exiba um exemplo em que , , sejam binárias, que seja um colisor e que, além disso, .
Exercício 2.40.
Seja Exiba um exemplo de sobre e grafos e sobre tais que e é compatível tanto com quanto com .
Exercício 2.41.
Seja uma densidade arbitrária sobre . Exiba um DAG sobre , , tal que é compatível com .
Exercício 2.42.
Exiba um exemplo em que é um colisor entre e , tem como único pai e e são dependentes dado .
Exercício 2.43.
Prove o Lema 2.26.