Capítulo 4 Resultados potenciais

No capítulo passado, vimos que $f(y|do(x))$ nos permite entender o comportamento de $Y$ em um cenário distinto dos dados observados. Por exemplo, se $X$ é a indicadora de um tratamento e $Y$ é a indicadora de cura, então $f(y|do(X=1))$ nos permite entender a proporção de cura em um cenário hipotético em que administramos o tratamento a todos os indivíduos. Esta distribuição nos permite investigar questões causais que não eram acessíveis usando apenas a distribuição observacional, $f(y,x)$ .

Contudo, algumas perguntas causais não são respondidas utilizando apenas os mecanismos desenvolvidos no capítulo 3. Por exemplo, qual a probabilidade de que um indivíduo se cure quando recebe o tratamento e não se cure quando não o recebe. Quando tentamos traduzir esta questão, notamos que partes dela envolvem $Y=1$ e $do(X=1)$ e outras partes envolvem $Y=0$ e $do(X=0)$ . Se tentarmos uma tradução ingênua, podemos obter uma expressão como ${\mathbb{P}}(Y=1,Y=0|do(X=1),do(X=0))$ . Contudo, a probabilidade acima não responde à pergunta colocada. Em primeiro lugar, não está definido fazermos as intervenções $do(X=1)$ e $do(X=0)$ na mesma unidade amostral. Além disso, mesmo que a probabilidade estivesse definida, é impossível que o mesmo $Y$ assuma tanto o valor $1$ quanto $0$ . Isto é, ${\mathbb{P}}(Y=1,Y=0|\ldots)=0$ .

A última constatação nos revela que o modelo no capítulo 3 não tem variáveis suficientes para traduzir a pergunta levantada. Se imaginamos que é possível que um indivíduo se cure ao receber o tratamento e não se cure quando não o recebe, isto ocorre pois as ocorrências de cura em cada cenário hipotético não são logicamente equivalentes. Em outras palavras, é como se houvessem resultados potenciais²² 2 Esta é uma tradução livre da expressão “potential outcomes” usada em inglês., $Y_{1}$ e $Y_{0}$ , para indicar a ocorrência de cura em cada cenário considerado. Com o uso destas variáveis, poderíamos escrever ${\mathbb{P}}(Y_{1}=1,Y_{0}=0)$ .

O objetivo desta seção é incluir este tipo de variável de forma a preservar as ferramentas desenvolvidas no capítulo 3.³³ 3 Para tal, adotaremos uma construção baseada em Galles1998. Neste quesito, a maior dificuldade será estabelecer a distribuição conjunta entre os resultados potenciais. Para tal, será útil relembrar um lema fundamental em simulação:

Lema 4.1.

Considere que $F(v|Pa(V))$ é uma função de densidade acumulada condicional arbitrária e $U\sim U(0,1)$ . Se definirmos, $V\equiv F^{-1}(U|Pa(V))$ , então $V|Pa(V)\sim F$ .

O Lema 4.1 traz várias interpretações que nos serão úteis. A primeira interpretação, de caráter técnico, é que podemos simular de qualquer distribuição multivariada utilizando apenas variáveis i.i.d. e funções determinísticas. Em particular, podemos reescrever um SCM de tal forma que cada vértice, $V$ , seja função determinística de seus pais e uma variável de ruído, $U_{V}$ . Esta abordagem, que está ligada a modelos de equações estruturais, é apresentada nas Definições 4.2 e 4.3.

Definição 4.2.

Seja ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$ um grafo causal. O grafo causal estrutural, ${\mathcal{G}}^{+}=({\mathcal{V}}^{+},{\mathcal{E}}^{+})$ , é tal que ${\mathcal{V}}^{+}={\mathcal{V}}\cup(U_{V})_{V\in{\mathcal{V}}}$ e ${\mathcal{E}}^{+}={\mathcal{E}}\cup\{(U_{V},V):V\in{\mathcal{V}}\}$ . Isto é, para cada $V\in{\mathcal{V}}$ , ${\mathcal{G}}^{+}$ adiciona uma nova variável $U_{V}$ e uma aresta de $U_{V}$ a $V$ .

Definição 4.3.

Seja $({\mathcal{G}},f)$ um CM. O Modelo Estrutural Causal (SCM) para $({\mathcal{G}},f)$ , $({\mathcal{G}}^{+},f^{+})$ , é tal que ${\mathcal{G}}^{+}$ é o grafo causal estrutural de ${\mathcal{G}}$ , $(U_{V})_{V\in{\mathcal{V}}}$ são independentes segundo $f^{+}$ e, para cada $V\in{\mathcal{V}}$ , existe uma função determinística, $g_{V}:U_{V}\times Pa(V)\rightarrow\Re$ , tal que $f^{+}(V|U_{V},Pa(V))={\mathbb{I}}(V=g_{V}(U_{V},Pa(V)))$ e $f^{+}({\mathcal{V}})=f({\mathcal{V}})$ .

O Exemplo 4.4 ilustra uma forma de obter um SCM em equações estruturais a partir de um SCM com dois vértices.

Exemplo 4.4.

Considere que $X\rightarrow Y$ , $X\sim\text{Exp}(1)$ e $Y|X\sim\text{Exp}(X)$ . Neste caso, o grafo estrutural causal é dado por $U_{X}\rightarrow X\rightarrow Y\leftarrow U_{Y}$ . Além disso, existem várias representações do SCM em equações estruturais. Uma possibilidade é definir que $U_{X}$ e $U_{Y}$ são i.i.d. e $U(0,1)$ , $X\equiv-\log(U_{X})$ e $Y\equiv-\log(U_{Y})/X$ .

O Lema 4.1 também permite uma interpretação de caráter mais filosófico. Podemos imaginar que toda variável em um SCM, $V$ , é uma função determinística de seus pais e de condições locais não-observadas, $U_{V}$ . A expressão “condições locais” indica que cada $U_{V}$ é usada somente para gerar $V$ e que as variáveis em $U$ são independentes, isto é, não trazem informação umas sobre as outras.

A interpretação acima é usada na definição de resultados potenciais. A ideia principal é que as mesmas funções determínistas e variáveis de ruído locais são usadas para gerar todos os resultados potenciais. A única diferença é que, para cada resultado potencial, o valor das variáveis em que houve intervenção é fixado. Esta definição é compatível com a ideia de que não é possível modificar os ruídos locais por meio da intervenção. Em outras palavras, o resultado potencial é o mais próximo possível do resultado observado sob a restrição que fixamos os valores das variáveis em que houve intervenção.

Definição 4.5.

Seja $({\mathcal{G}},f)$ um CM de grafo causal ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$ e $({\mathcal{G}}^{+},f^{+})$ o seu SCM. O grafo de resultados potenciais dado por intervenções em ${\mathbf{X}}\subseteq{\mathcal{V}}$ , ${\mathcal{G}}^{*}=({\mathcal{V}}^{*},{\mathcal{E}}^{*})$ é tal que

	$\displaystyle{\mathcal{V}}^{*}$	$\displaystyle=\{W_{{\mathbb{V}}={\mathbf{v}}}:W\in{\mathcal{V}},{\mathbb{V}}% \subseteq{\mathbf{X}},{\mathbf{v}}\in supp({\mathbb{V}})\}\cup\{U_{W}:W\in{% \mathcal{V}}\},$
	$\displaystyle{\mathcal{E}}^{*}$	$\displaystyle=\{(W_{{\mathbb{V}}={\mathbf{v}}},Z_{{\mathbb{V}}={\mathbf{v}}}):% {\mathbb{V}}\subseteq{\mathbf{X}},{\mathbf{v}}\in supp({\mathbb{V}}),(W,Z)\in{% \mathcal{E}}^{+},Z\notin{\mathbb{V}}\}.$

Para todo $W\in{\mathcal{V}}$ , abreviamos $W_{\emptyset}$ por $W$ .

Em palavras, o grafo de resultados potenciais cria uma cópia de ${\mathcal{G}}$ para cada possível intervenção, ${\mathbb{V}}={\mathbf{v}}$ . Além disso, adiciona-se uma aresta de $U_{W}$ para cada cópia de $W$ . Esta construção indica que as mesmas variáveis em $U$ geram todos os resultados potenciais. Também, para cada vértice em que houve uma intervenção, $W_{{\mathbb{V}}={\mathbf{v}}}\in{\mathbb{V}}_{{\mathbb{V}}={\mathbf{v}}}$ , removem-se todas as arestas que apontam para $W_{{\mathbb{V}}={\mathbf{v}}}$ . Esta remoção ocorre porque, quando realizamos uma intervenção em ${\mathbb{V}}$ o valor desta variável é fixado e, assim, não é gerado por suas causas em ${\mathcal{G}}$ .

Exemplo 4.6.

Considere que $(X,Y)\in\{0,1\}^{2}$ e o grafo causal é $X\rightarrow Y$ . Vimos no Exemplo 4.4 que o grafo causal estrutural é dado por $U_{X}\rightarrow X\rightarrow Y\leftarrow U_{Y}$ . Vamos construir o grafo de resultados potenciais dadas intervenções em $X$ . Neste caso, além dos vértices $U_{X},U_{Y},X,Y$ , temos também $X_{X=0},Y_{X=0},X_{X=1},Y_{X=1}$ . Como não há ambiguidade neste caso, podemos abreviar os últimos quatro vértices por $X_{0},Y_{0},X_{1},Y_{1}$ .

O grafo de resultados potenciais é ilustrado na figur 16. O grafo causal estrutural é a reta horizontal de $U_{X}$ a $U_{Y}$ . Os resultados potenciais são cópias deste grafo que usam as mesmas variáveis $U$ e em que removemos as arestas que apontam para a intervenções, $X_{0}$ e $X_{1}$ .

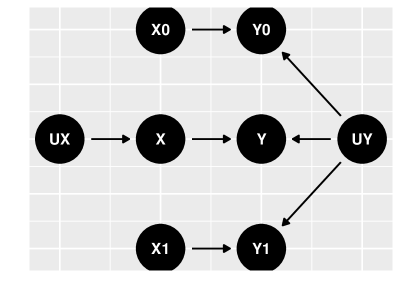
Refer to caption — Figura 16: Grafo de resultados potenciais dadas intervenções em $X\in\{0,1\}$ .

Uma vez definido o grafo de resultados potenciais, podemos extender a distribuição do modelo de equações estruturais para este grafo. Esta extensão envolve três etapas. Primeiramente, a distribuição de $U$ continua a mesma. Em segundo lugar, para todo vértice do grafo de resultados potenciais, $W_{{\mathbb{V}}={\mathbf{v}}}$ , em que não houve uma intervenção, este vértice é gerado pelo mesmo mecanismo que $W$ . Isto é, $W_{{\mathbb{V}}={\mathbf{v}}}={\mathbb{I}}(g_{W}(U_{W},Pa^{*}(W_{{\mathbb{V}}=% {\mathbf{v}}})))$ . Finalmente, se houve uma intervenção em $W_{{\mathbb{V}}={\mathbf{v}}}$ , então ela é uma variável degenerada no valor desta intervenção. Esta construção é formalizada na Definição 4.7.

Definição 4.7.

Seja $({\mathcal{G}}^{+},f^{+})$ um SCM para $({\mathcal{G}},f)$ com funções determinísticas, $g$ . O modelo de resultados potenciais (POM)⁴⁴ 4 utilizamos a sigla POM em referência ao termo em inglês “potential outcomes model” dado por intervenções em ${\mathbf{X}}$ , é um modelo probabilístico em um DAG, $({\mathcal{G}}^{*},f^{*})$ , tal que ${\mathcal{G}}^{*}$ é o grafo de resultados potenciais dado por intervenções em ${\mathbf{X}}$ (Definição 4.5) e

	$\displaystyle f^{*}(U_{W})$	$\displaystyle=f(U_{W})$	$\displaystyle\text{, para todo }W\in{\mathcal{V}},$
	$\displaystyle f^{}(W_{{\mathbb{V}}={\mathbf{v}}}\|Pa^{}(W_{{\mathbb{V}}={% \mathbf{v}}}))$	$\displaystyle=\begin{cases}{\mathbb{I}}(W_{{\mathbb{V}}={\mathbf{v}}}={\mathbf% {v}}_{i})&\text{, se }W\equiv{\mathbb{V}}_{i}\\ {\mathbb{I}}(W_{{\mathbb{V}}={\mathbf{v}}}=g_{W}(U_{W},Pa^{*}(W_{{\mathbb{V}}=% {\mathbf{v}}})))&\text{, caso contrário.}\end{cases}$

O Exemplo 4.8 ilustra um modelo de resultados potenciais.

Exemplo 4.8.

Considere o SCM em equações estruturais em Exemplo 4.4. Na construção do modelo de resultados potenciais, definimos $X,Y,U_{X},U_{Y}$ igualmente a em Exemplo 4.4. Além disso, para cada $x>0$ , $X_{x}\equiv x$ e $Y_{x}\equiv-log(U_{Y})/X_{x}$ .