3 Independência Condicional e D-separação

Independência condicional é uma forma fundamental de indicar relações entre variáveis aleatórias. Se ${\mathbf{X}}_{1},\ldots,{\mathbf{X}}_{d}$ e ${\mathbf{Y}}$ são vetores de variáveis aleatórias, definimos que $({\mathbf{X}}_{1},\ldots,{\mathbf{X}}_{d})|{\mathbf{Y}}$ , isto é, ${\mathbf{X}}_{1},\ldots,{\mathbf{X}}_{d}$ são independentes dado ${\mathbf{Y}}$ , se conhecido o valor de ${\mathbf{Y}}$ , observar quaisquer valores de ${\mathbf{X}}$ não traz informação sobre os demais valores. Nesta seção veremos que as relações de independência condicional em um CM estão diretamente ligadas ao seu grafo.

3.1 Independência Condicional

Definição 2.44.

Dizemos que $({\mathbf{X}}_{1},\ldots,{\mathbf{X}}_{d})$ são independentes dado ${\mathbf{Y}}$ se, para qualquer ${\mathbf{x}}_{1},\ldots,{\mathbf{x}}_{n}$ e ${\mathbf{y}}$ ,

\displaystyle f({\mathbf{x}}_{1},\ldots,{\mathbf{x}}_{n}|{\mathbf{y}})

\displaystyle=\prod_{i=1}^{d}f({\mathbf{x}}_{i}|{\mathbf{y}})

Em particular, $({\mathbf{X}}_{1},\ldots,{\mathbf{X}}_{d})$ são independentes se, para quaiquer $({\mathbf{x}}_{1},\ldots,{\mathbf{x}}_{d})$ ,

\displaystyle f({\mathbf{x}}_{1},\ldots,{\mathbf{x}}_{d})

\displaystyle=\prod_{i=1}^{d}f({\mathbf{x}}_{i})

Verificar se a Definição 2.44 está satisfeita nem sempre é fácil. A princípio, ela exige obter tanto a distribuição condicional conjunta, $f({\mathbf{x}}_{1},\ldots,{\mathbf{x}}_{d}|{\mathbf{y}})$ , quanto cada uma das marginais, $f({\mathbf{x}}_{i}|{\mathbf{y}})$ . O Lema 2.45 a seguir apresenta outras condições que são equivalentes a independência condicional:

Lema 2.45.

As seguintes afirmações são equivalentes:

1.

$({\mathbf{X}}_{1},\ldots,{\mathbf{X}}_{d})$ são independentes dado ${\mathbf{Y}}$ ,
2.

Existem funções, $h_{1},\ldots,h_{d}$ tais que $f({\mathbf{x}}_{1},\ldots,{\mathbf{x}}_{d}|{\mathbf{y}})=\prod_{j=1}^{d}{h_{j}% ({\mathbf{x}}_{j},{\mathbf{y}})}$ .
3.

Para todo $i$ , $f({\mathbf{x}}_{i}|{\mathbf{x}}_{-i},{\mathbf{y}})=f({\mathbf{x}}_{i}|{\mathbf% {y}})$ .
4.

Para todo $i$ , $f({\mathbf{x}}_{i}|{\mathbf{x}}_{1}^{i-1},{\mathbf{y}})=f({\mathbf{x}}_{i}|{% \mathbf{y}})$ .

As condições no Lema 2.45 são, em geral, mais fáceis de verificar do que a definição direta de independência condicional. A seguir veremos que, em um SMC, pode ser mais fácil ainda verificar muitas das relações de independência condicional.

3.2 D-separação

Em um CM , é possível indicar as relações de independência incondicional em ${\mathcal{V}}$ por meio do grafo associado. Intuitivamente, haverá uma dependência entre $V_{1}$ e $V_{2}$ se for possível transmitir a informação de $V_{1}$ para $V_{2}$ por um caminho que ligue ambos os vértices. Para entender se a informação pode ser transmitida por um caminho, classificaremos a seguir os vértices que o constituem.

Definição 2.46.

Seja $C=(C_{1},\ldots,C_{n})$ um caminho em um DAG, ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$ . Para cada $2\leq i\leq n-1$ :

•

$C_{i}$ é um colisor em $C$ se $(C_{i-1},C_{i})\in{\mathcal{E}}$ e $(C_{i+1},C_{i})\in{\mathcal{E}}$ , isto é, existem arestas apontando de $C_{i-1}$ e de $C_{i+1}$ para $C_{i}$ . Neste caso, desenhamos $C_{i-1}\rightarrow C_{i}\leftarrow C_{i+1}$ .

Note que a classificação na Definição 2.46 generaliza os exemplos de DAG’s com 3 vértices na Seção 2.4.

Essa classificação é ilustrada com o DAG na figur 5. Existem dois caminhos que vão de $V_{1}$ a $V_{4}$ : $V_{1}\rightarrow V_{2}\leftarrow V_{4}$ e $V_{1}\rightarrow V_{2}\rightarrow V_{3}\leftarrow V_{4}$ . No primeiro caminho $V_{2}$ é um colisor, pois o caminho passa por duas arestas que apontam para $V_{2}$ . Já no segundo caminho $V_{2}$ é uma cadeia e $V_{3}$ é um colisor. Note que a classificação do vértice depende do caminho analisado. Enquanto que no primeiro caminho $V_{2}$ é um colisor, no segundo $V_{2}$ é uma cadeia

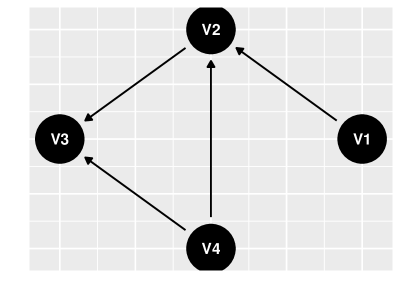
Refer to caption — Figura 5: Ilustração do conceito de bloqueio de um caminho. No caminho (V1, V2, V4), V2 é um colisor. Isto ocorre pois, para chegar de V1 a V4 passando apenas por V2, as duas arestas apontam para V2. Já no caminho (V1, V2, V3, V4) temos que V2 é uma cadeia. Para chegar de V1 a V3 passando por V2, passa-se por duas arestas, uma entrando e outra saindo de V2. Como V2 é um colisor em (V1, V2, V4), este caminho está bloqueado se e somente se o valor de V2 é desconhecido. Como V2 é uma cadeia em (V1, V2, V3, V4), esse caminho está bloqueado quando o valor de V2 é conhecido.

Com base nas conclusões da Seção 2.4, é possível compreender a racionalidade da Definição 2.46. Na Seção 2.4 vimos que, se $Z$ não é um colisor entre $X$ e $Y$ , então $X$ e $Y$ são independentes dado $Z$ . Por analogia, podemos intuir que um vértice que não é um colisor num caminho não permite a passagem de informação quando seu valor é conhecido. Similarmente, na Seção 2.4, se $Z$ é um colisor entre $X$ e $Y$ , então $X$ e $Y$ são independentes. Assim, também podemos intuir que um vértice que é um colisor em um caminho não permite a passagem de informação quando seu valor e o de seus descendentes é desconhecido. Finalmente, a informação não passa pelo caminho quando ela não passa por pelo menos um de seus vértices. Neste caso, dizemos que o caminho está bloqueado:

Definição 2.47.

Seja $C=(C_{1},\ldots,C_{n})$ um caminho em um DAG, ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$ . Dizemos que $C$ está bloqueado dado ${\mathbf{Z}}\subset{\mathcal{V}}$ , se

1.

Existe algum $2\leq i\leq n-1$ tal que $C_{i}$ não é um colisor em $C$ e $C_{i}\in{\mathbf{Z}}$ , ou
2.

Existe algum $2\leq i\leq n-1$ tal que $C_{i}$ é um colisor em $C$ e $C_{i}\notin Anc({\mathbf{Z}})$ .

Finalmente, dizemos que ${\mathbb{V}}_{1}$ está d-separado de ${\mathbb{V}}_{2}$ dado ${\mathbb{V}}_{3}$ se todos os caminhos de ${\mathbb{V}}_{1}$ a ${\mathbb{V}}_{2}$ estão bloqueados dado ${\mathbb{V}}_{3}$ :

Definição 2.48.

Seja ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$ um DAG. Para ${\mathbb{V}}_{1},{\mathbb{V}}_{2},{\mathbb{V}}_{3}\subseteq{\mathcal{V}}$ , dizemos que ${\mathbb{V}}_{1}$ está d-separado de ${\mathbb{V}}_{2}$ dado ${\mathbb{V}}_{3}$ se, para todo caminho $C=(C_{1},\ldots,C_{n})$ tal que $C_{1}\in V_{1}$ e $C_{n}\in{\mathbb{V}}_{2}$ , $C$ está bloqueado dado ${\mathbb{V}}_{3}$ . Neste caso, escrevemos ${\mathbb{V}}_{1}\perp{\mathbb{V}}_{2}|{\mathbb{V}}_{3}$ .

Intuitivamente, se ${\mathbb{V}}_{1}\perp{\mathbb{V}}_{2}|{\mathbb{V}}_{3}$ , então não é possível passar informação de ${\mathbb{V}}_{1}$ a ${\mathbb{V}}_{2}$ quando ${\mathbb{V}}_{3}$ é conhecido. Assim, temos razão para acreditar que ${\mathbb{V}}_{1}$ é condicionalmente independente de ${\mathbb{V}}_{2}$ dado ${\mathbb{V}}_{3}$ , isto é ${\mathbb{V}}_{1}\perp\!\!\!\!\perp{\mathbb{V}}_{2}|{\mathbb{V}}_{3}$ . Esta conclusão é apresentada no Teorema 2.49 a seguir:

Teorema 2.49.

Seja ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$ um DAG e ${\mathcal{V}}$ um conjunto de variáveis aleatórias. ${\mathbb{V}}_{1}$ está d-separado de ${\mathbb{V}}_{2}$ dado ${\mathbb{V}}_{3}$ se e somente se, para todo $f$ compatível com ${\mathcal{G}}$ , ${\mathbb{V}}_{1}\perp\!\!\!\!\perp^{f}{\mathbb{V}}_{2}|{\mathbb{V}}_{3}$ .

Exemplo 2.50.

Considere o DAG na figur 5. Para avaliar se $V_{1}$ e $V_{3}$ são d-separados, precisamos analisar todos os caminhos de um para o outro. Estes caminhos são: $V_{1}\rightarrow V_{2}\rightarrow V_{3}$ , e $V_{1}\rightarrow V_{2}\leftarrow V_{4}\rightarrow V_{3}$ . No primeiro caminho $V_{2}$ não é um colisor e, assim, o caminho não está bloqueado marginalmente. Portanto, $V_{1}$ e $V_{3}$ não são d-separados marginalmente. Por outro lado, no segundo caminho $V_{2}$ é um colisor e $V_{4}$ não o é. Assim, condicionando em $V_{2}$ , este caminho não está bloqueado. Portanto, $V_{1}$ e $V_{3}$ não são d-separados dado $V_{2}$ . Finalmente, dado $V_{2}$ e $V_{4}$ , ambos os caminhos estão bloqueados, pois $V_{2}$ não é um colisor no primeiro e $V_{4}$ não é um colisor no segundo. Assim, $V_{1}$ e $V_{3}$ são d-separados dado $(V_{2},V_{4})$ . Para treinar este raciocínio, continue analisando a d-separação entre $V_{1}$ e $V_{4}$ .

O algoritmo para testar d-separação está implementado em diversos pacotes. Além disso, é possível utilizar o Teorema 2.49 para enunciar todas as relações de independência condicional que são necessárias em um grafo. Estas implementações estão ilustradas abaixo: \MakeFramed

# Especificar o grafo
grafo <- "dag{
   V1 -> V2 <- V4;
   V2 -> V3 <- V4
}"

dseparated(grafo, "V1", "V3", c("V2"))

## [1] FALSE

dseparated(grafo, "V1", "V3", c("V4"))

## [1] FALSE

dseparated(grafo, "V1", "V3", c("V2", "V4"))

## [1] TRUE

impliedConditionalIndependencies(grafo)

## V1 _||_ V3 | V2, V4
## V1 _||_ V4

\endMakeFramed

Exemplo 2.51.

Considere que ${\mathbb{V}}_{1}$ e ${\mathbb{V}}_{2}$ não são d-separados dado ${\mathbb{V}}_{3}$ . O Teorema 2.49 garante apenas que existe algum $f$ compatível com o DAG tal que ${\mathbb{V}}_{1}$ e ${\mathbb{V}}_{2}$ são condicionalmente dependentes dado ${\mathbb{V}}_{3}$ segundo $f$ . É possível mostrar que o conjunto de $f$ ’s compatíveis com o grafo em que ${\mathbb{V}}_{1}$ e ${\mathbb{V}}_{2}$ são condicionalmente independentes dado ${\mathbb{V}}_{3}$ é relativamente pequeno àquele em que ${\mathbb{V}}_{1}$ e ${\mathbb{V}}_{2}$ são condicionalmente dependentes. Estudaremos um caso em que é possível observar esta relação em mais detalhe.

Considere que $V_{1},V_{2}$ , e $Z$ são binárias e formam o grafo $V_{1}\leftarrow Z\rightarrow V_{2}$ , isto é, $Z$ é um confundidor. Além disso, ${\mathbb{P}}(Z=1)=0.5$ , ${\mathbb{P}}(V_{i}=1|Z=j)=:p_{j}$ . Como $V_{3}$ é um confundidor, $V_{1}$ e $V_{2}$ não são d-separados marginalmente. Para quais valores de $p$ temos que $V_{1}$ e $V_{2}$ são marginalmente independentes? Para que $V_{1}$ e $V_{2}$ sejam independentes, é necessário que $Cov[V_{1},V_{2}]=0$ . Note que

	$\displaystyle{\mathbb{E}}[V_{i}]$	$\displaystyle={\mathbb{E}}[{\mathbb{E}}[V_{i}\|Z]]=0.5p_{1}+0.5p_{0}$
	$\displaystyle{\mathbb{E}}[V_{1}V_{2}]$	$\displaystyle={\mathbb{E}}[\|E[V_{1}V_{2}\|Z]]=0.5p_{1}^{2}+0.5p_{0}^{2}$

Assim, para que $Cov[V_{1},V_{2}]=0$ , temos:

	$\displaystyle 0.5p^{2}_{1}+0.5p^{2}_{0}$	$\displaystyle=(0.5p_{1}+0.5p_{0})(0.5p_{1}+0.5p_{0})$
	$\displaystyle 0.5p^{2}_{1}+0.5p^{2}_{0}$	$\displaystyle=0.25p_{1}^{2}++0.5p_{1}p_{0}0.25p_{0}^{2}$
	$\displaystyle 0.25p^{2}_{1}-0.5p_{1}p_{0}+0.25p^{2}_{0}$	$\displaystyle=0$
	$\displaystyle 0.25(p_{1}-p_{0})^{2}$	$\displaystyle=0$
	$\displaystyle p_{1}$	$\displaystyle=p_{0}$

Em outras palavras, dentre todos $(p_{0},p_{1})$ no quadrado $[0,1]^{2}$ , somente os valores no segmento $p_{1}=p_{0}$ tem alguma chance de levarem à independência entre $V_{1}$ e $V_{2}$ . Se imaginarmos que $(p_{0},p_{1})$ são equidistribuídos em $[0,1]^{2}$ , então a probabilidade de sortearmos valores em que $V_{1}$ e $V_{2}$ são independentes é 0.

Em conclusão, como $V_{1}$ e $V_{2}$ não são d-separados, somente para um conjunto pequeno de possíveis $f$ ’s temos que $V_{1}$ e $V_{2}$ são independentes.

3.3 Exercícios

Exercício 2.52.

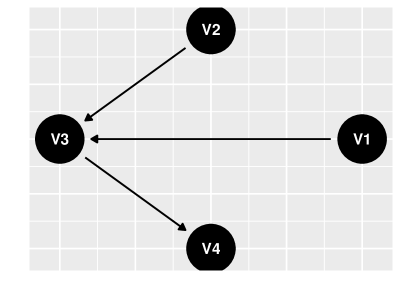
Considere que $f$ é uma densidade sobre ${\mathcal{V}}=(V_{1},V_{2},V_{3},V_{4})$ que é compatível com o grafo em figur 6. Além disso, cada $V_{i}\in\{0,1\}$ , $V_{1},V_{2}\sim\text{Bernoulli}(0.5)$ , $V_{3}\equiv V_{1}\cdot V_{2}$ e ${\mathbb{P}}(V_{4}=i|V_{3}=i)=0.9$ , para todo $i$ .

(a)

$V_{1}$ e $V_{2}$ são d-separados dado $V_{3}$ ?
(b)

$V_{1}$ e $V_{2}$ são condicionalmente independentes dado $V_{3}$ ?
(c)

$V_{1}$ e $V_{2}$ são d-separados dado $V_{4}$ ?
(d)

$V_{1}$ e $V_{2}$ são condicionalmente independentes dado $V_{4}$ ?

Exercício 2.53.

Prove que se um caminho, $C=(C_{1},\ldots,C_{n})$ , está bloqueado dado ${\mathbb{V}}$ , então sempre que $C$ é um sub-caminho de $C^{*}$ , isto é, $C^{*}=(A_{1},\ldots,A_{m},C_{1},\ldots,C_{n},B_{1},\ldots,B_{l})$ , temos que $C^{*}$ está bloqueado dado ${\mathbb{V}}$ .

Exercício 2.54.

Prove que se ${\mathbb{V}}_{1}\perp{\mathbb{V}}_{3}|{\mathbb{V}}_{4}$ e ${\mathbb{V}}_{2}\perp{\mathbb{V}}_{3}|{\mathbb{V}}_{4}$ , então ${\mathbb{V}}_{1}\cup{\mathbb{V}}_{2}\perp{\mathbb{V}}_{3}|{\mathbb{V}}_{4}$ .

Exercício 2.55.

Prove que se ${\mathbb{V}}_{1}\perp{\mathbb{V}}_{2}|{\mathbb{V}}_{3}$ , então para todo $V\in(Anc({\mathbb{V}}_{3})-{\mathbb{V}}_{3})$ , $V\perp{\mathbb{V}}_{1}|{\mathbb{V}}_{3}$ ou $V\perp{\mathbb{V}}_{2}|{\mathbb{V}}_{3}$ .

Exercício 2.56.

Sejam ${\mathcal{G}}_{1}=({\mathcal{V}},{\mathcal{E}}_{1})$ e ${\mathcal{G}}_{2}=({\mathcal{V}},{\mathcal{E}}_{2})$ grafos tais que ${\mathcal{E}}_{1}\subseteq{\mathcal{E}}_{2}$ . Prove que se ${\mathbb{V}}_{1}\perp^{d}{\mathbb{V}}_{2}|{\mathbb{V}}_{3}$ em ${\mathcal{G}}_{2}$ , então ${\mathbb{V}}_{1}\perp^{d}{\mathbb{V}}_{2}|{\mathbb{V}}_{3}$ em ${\mathcal{G}}_{1}$ .