5 Controlando confundidores (critério backdoor)

Um confundidor é uma causa comum, direta ou indireta, de $X$ em $Y$ . Na existência de confundidores, a regressão de $Y$ em $X$ no modelo observacional, ${\mathbb{E}}[Y|X]$ , é diferente desta regressão no modelo de intervenção, ${\mathbb{E}}[Y|do(X)]$ . Isto ocorre pois, quando calculamos ${\mathbb{E}}[Y|X]$ , utilizamos toda a informação em $X$ para prever $Y$ . Esta informação inclui não apenas o efeito causal de $X$ em $Y$ , como também a informação que $X$ traz indiretamente sobre $Y$ pelo fato de ambas estarem associados aos seus confundidores.

Para ilustrar este raciocínio, podemos revisitar o Exemplo 3.5. uma vez que Sexo (Z) é causa comum do Tratamento (X) e da Cura (Y), Z é um confundidor. Quando calculamos $f(y|x)$ (Seção 4), utilizamos não só o efeito direto de $X$ em $Y$ , expresso em $f(y|x,z)$ , como também a informação que indireta que $X$ traz sobre $Y$ por meio do confundidor $Z$ , expressa pela combinação de $f(z|x)$ com $f(y|x,z)$ .

Esta seção desenvolve uma estratégia para medir o efeito causal chamada de critério backdoor, que consiste em bloquear todos os caminhos de informação que passam por confundidores:

Definição 3.11.

Seja ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$ um grafo causal e $X,Y\in{\mathcal{V}}$ . Dizemos que ${\mathbf{Z}}\subseteq{\mathcal{V}}-\{X,Y\}$ satisfaz o critério “backdoor” se:

1.

$X\notin Anc({\mathbf{Z}})$ ,
2.

Para todo caminho de $X$ em $Y$ , $C=(X,C_{2},\ldots,C_{n-1},Y)$ tal que $(C_{2},X)\in{\mathcal{E}}$ , $C$ está bloqueado dado ${\mathbf{Z}}$ .

Exemplo 3.12.

No Exemplo 3.5 o único caminho de $X$ em $Y$ em que o vértice ligado a $X$ é pai de $X$ é $X\leftarrow Z\rightarrow Y$ . Como $Z$ é um confudidor neste caminho, ele o bloqueia. Assim, $Z$ satisfaz o critério backdoor.

Exemplo 3.13.

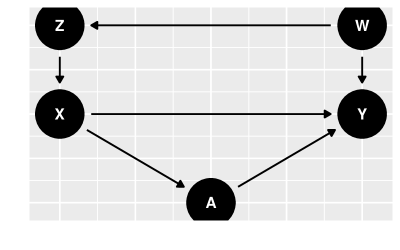
Refer to caption — Figura 10: Para medir o efeito causal de X em Y, podemos aplicar o critério backdoor. Neste grafo o único caminho aplicável ao critério backdoor é (X, Z, W, Y). Neste caminho, $Z$ é uma cadeia e $W$ é um confundidor. Assim, todas as possibilidades dentre Z, W, (Z,W) bloqueiam o caminho e satisfazem o critério backdoor.

Considere o grafo causal na figur 10. Para aplicar o critério backdoor, devemos identificar todos os caminhos de $X$ em $Y$ em que o vértice ligado a $X$ é pai de $X$ , isto é, temos $X\leftarrow$ . O único caminho deste tipo é: $X\leftarrow Z\leftarrow W\rightarrow Y$ . Neste caminho, $Z$ é uma cadeia e $W$ é um confudidor. Assim, é possível bloquear este caminho condicionando em $Z$ , em $W$ , e em $(Z,W)$ . Isto é, todos estas combinações satisfazem o critério backdoor.

Exemplo 3.14.

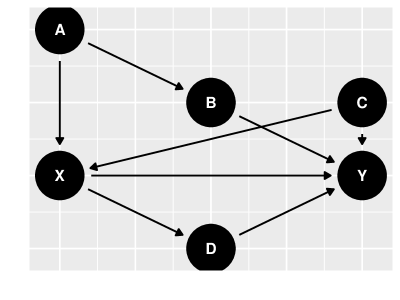
Considere o grafo causal na figur 11. Para aplicar o critério backdoor, encontramos todos os caminhos de $X$ em $Y$ em que o vértice ligado a $X$ é pai de $X$ . Há dois caminhos deste tipo: $X\leftarrow A\rightarrow B\rightarrow Y$ e $X\leftarrow C\rightarrow Y$ . Como $A$ e $C$ são confudidores, respectivamente, no primeiro e segundo caminhos, $(A,C)$ bloqueia ambos eles. Assim $(A,C)$ satisfaz o critério backdoor. Você consegue encontrar outro conjunto de variáveis que satisfaz o critério backdoor?

Também é possível identificar os conjuntos de variáveis que satisfazem o critério backdoor por meio do pacote dagitty, como ilustrado a seguir:

\MakeFramed

library(dagitty)
# Especificar o grafo
grafo <- dagitty("dag{
    X[e] Y[o]
    A -> { X B }; B -> { Y }; C -> { X Y };
    X -> { D Y }; D -> Y }")

adjustmentSets(grafo, type = "all")

## { A, C }
## { B, C }
## { A, B, C }

\endMakeFramed

O critério backdoor generaliza duas condições especiais que são muito utilizadas. Em uma primeira condição, o valor de $X$ é gerado integralmente por um aleatorizador, independente de todas as demais variáveis. Esta ideia é captada pela Definição 3.15, abaixo:

Definição 3.15.

Dizemos que $X$ é um experimento aleatorizado simples se $X$ é ancestral.

Em um experimento aleatorizado simples não há confundidores. Assim, $\emptyset$ satisfaz o critério backdoor:

Lema 3.16.

Se $X$ é um experimento aleatorizado simples, então $\emptyset$ satisfaz o critério backdoor.

Veremos que em um experimento aleatorizado simples a distribuição intervencional é igual à distribuição observacional. Assim, ${\mathbb{E}}[Y|do(X)]={\mathbb{E}}[Y|X]$ e a inferência causal é reduzida à inferência comumente usadas para a distribuição observacional.

Além disso, o conjunto de todos os pais de $X$ também satisfaz o critério backdoor:

Lema 3.17.

${\mathbf{Z}}=Pa(X)$ satisfaz o critério backdoor para medir o efeito causal de $X$ em $Y$ .

A seguir, veremos como o critério backdoor permite a identificação causal, isto é, uma equivalência entre quantidades de interesse obtidas pelo modelo de intervenção e quantidades obtidas pelo modelo observacional.

5.1 Identificação causal usando o critério backdoor

A seguir, o Teorema 3.19 mostra que, se ${\mathbf{Z}}$ satisfaz o critério backdoor, então é possível ligar algumas distribuições sob intervenção em $X$ a distribuições observacionais:

Definição 3.18.

${\mathbf{Z}}$ controla confundidores para medir o efeito causal de $X$ em $Y$ se

	$\displaystyle f({\mathbf{z}}\|do(x))$	$\displaystyle=f({\mathbf{z}}),\text{ e }$
	$\displaystyle f(y\|do(x),{\mathbf{z}})$	$\displaystyle=f(y\|x,{\mathbf{z}}).$

Teorema 3.19.

Se ${\mathbf{Z}}$ satisfaz o critério backdoor para medir o efeito causal de $X$ em $Y$ , então ${\mathbf{Z}}$ satisfaz a Definição 3.18.

O Teorema 3.19 mostra que, se ${\mathbf{Z}}$ satisfaz o critério backdoor, então distribuição de ${\mathbf{Z}}$ quando aplicamos uma intervenção em $X$ é igual à distribuição marginal de ${\mathbf{Z}}$ . Além disso, a distribuição condicional de $Y$ dado ${\mathbf{Z}}$ quando aplicamos uma intervenção em $X$ é igual à distribuição de $Y$ dado $X$ e $Z$ . Assim, o Teorema 3.19 relaciona distribuições que não geraram os dados a distribuições que os geraram. Com base neste resultado, é possível determinar $f(y|do(x))$ a partir de $f(y,x,{\mathbf{z}})$ :

Corolário 3.20.

Se ${\mathbf{Z}}$ satisfaz a Definição 3.18, então

\displaystyle f(y|do(x))

\displaystyle=\int f(y|x,{\mathbf{z}})f({\mathbf{z}})d{\mathbf{z}}.

Para compreender intuitivamente o Corolário 3.20, podemos retornar ao Exemplo 3.5. Considere o caso em que $X,Y,Z$ são as indicadoras de que, respectivamente, o paciente foi submetido ao tratamento, se curou e, é de sexo masculino. Similarmente ao Teorema 3.19, vimos em Exemplo 3.5 que $f(y|do(x))$ é a média de $f(y|x,z)$ ponderada por $f(z)$ . Nesta ponderação, utilizamos $f(z)$ ao invés de $f(z|x)$ pois $Z$ é um confundidor e, assim, no modelo intervencional não propagamos a informação em $X$ por esta variável. A mesma lógica se aplica às variáveis que satisfazem o critério backdoor.

Para calcular quantidades como o ${ACE}$ (Definição 3.4), utilizamos ${\mathbb{E}}[Y|do(X)]$ . Por meio do Teorema 3.19, é possível obter equivalências entre ${\mathbb{E}}[Y|do(X)]$ e esperanças obtidas no modelo observacional. Estas equivalências são descritas nos Teoremas 3.21 e 3.22.

Teorema 3.21.

Se ${\mathbf{Z}}$ satisfaz a Definição 3.18, então

	$\displaystyle{\mathbb{E}}[g(Y)\|do(X=x),{\mathbf{Z}}]$	$\displaystyle={\mathbb{E}}[g(Y)\|X=x,{\mathbf{Z}}],\text{ e }$
	$\displaystyle{\mathbb{E}}[g(Y)\|do(X=x)]$	$\displaystyle={\mathbb{E}}[{\mathbb{E}}[g(Y)\|X=x,{\mathbf{Z}}]]$

Teorema 3.22.

Se ${\mathbf{Z}}$ satisfaz a Definição 3.18 e $X$ é discreto, então

	$\displaystyle{\mathbb{E}}[g(Y)\|do(X=x),{\mathbf{Z}}]$	$\displaystyle=\frac{{\mathbb{E}}[g(Y){\mathbb{I}}(X=x)\|{\mathbf{Z}}]}{f(x\|{% \mathbf{Z}})},\text{ e }$
	$\displaystyle{\mathbb{E}}[g(Y)\|do(X=x)]$	$\displaystyle={\mathbb{E}}\left[\frac{g(Y){\mathbb{I}}(X=x)}{f(x\|{\mathbf{Z}})% }\right]$

A seguir, veremos como os Teoremas 3.21 e 3.22 podem ser usados para estimar o efeito causal. Para provar resultados sobre os estimadores obtidos, a seguinte definição será útil

Definição 3.23.

Seja $\hat{g}$ um estimador treinado com os dados $({\mathcal{V}}_{1},\ldots,{\mathcal{V}}_{n})$ . Dizemos que $\hat{g}$ é invariante a permutações se o estimador não depende da ordem dos dados. Isto é, para qualquer permutações dos índices, $\pi:\{1,\ldots,n\}\rightarrow\{1,\ldots,n\}$ , $\hat{g}({\mathcal{V}}_{1},\ldots,{\mathcal{V}}_{n})\equiv\hat{g}({\mathcal{V}}% _{\pi(1)},\ldots,{\mathcal{V}}_{\pi(n)})$

Exemplo 3.24.

A média amostral é invariante a permutações pois, para qualquer permutação $\pi$ ,

\displaystyle\frac{\sum_{i=1}^{n}X_{i}}{n}=\frac{\sum_{i=1}^{n}X_{\pi(i)}}{n}.

5.2 Estimação usando o critério backdoor

5.2.1 Fórmula do ajuste

Se ${\mathbf{Z}}$ satisfaz a Definição 3.18, então ${\mathbb{E}}[Y|do(X),{\mathbf{Z}}]={\mathbb{E}}[Y|X,{\mathbf{Z}}]$ . Como $\mu(X,Z):={\mathbb{E}}[Y|X,{\mathbf{Z}}]$ é a função de regressão de $Y$ em $X$ e $Z$ , podemos estimar $\mu$ utilizando quaisquer métodos de estimação para regressão. Por exemplo, se $Y$ é contínua, possíveis métodos são: regressão linear, Nadaraya-Watson, floresta aleatória de regressão, redes neurais, …Por outro lado, se $Y$ é discreta, então a função de regressão é estimada por métodos de classificação como: regressão logística, k-NN, floresta aleatória de classificação, redes neurais, …Para qualquer opção escolhida, denotamos o estimador de $\mu$ por ${\widehat{\mu}}$ .

Utilizando ${\widehat{\mu}}$ , podemos estimar ${CACE}({\mathbf{Z}})$ diretamente. Para tal, note que ${CACE}({\mathbf{Z}})$ é função de ${\mathbb{E}}[Y|do(X),{\mathbf{Z}}]$ . Como o Teorema 3.21 garante que ${\mathbb{E}}[Y|do(X=x),{\mathbf{Z}}]=\mu(x,{\mathbf{Z}})$ , podemos definir o estimador

\displaystyle{\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x),{\mathbf{Z}}]:={\widehat{% \mu}}(x,{\mathbf{Z}}).

O Teorema 3.21 também orienta a estimação do ${ACE}$ . Similarmente ao caso anterior, o ${ACE}$ é função de ${\mathbb{E}}[Y|do(X)]$ . Pelo Teorema 3.21, ${\mathbb{E}}[Y|do(X=x)]={\mathbb{E}}[\mu(x,{\mathbf{Z}})]$ . Assim, se ${\widehat{\mu}}\approx\mu$ , ${\mathbb{E}}[Y|do(X=x)]\approx{\mathbb{E}}[{\widehat{\mu}}(x,{\mathbf{Z}})]$ . Como ${\mathbb{E}}[{\widehat{\mu}}(x,{\mathbf{Z}})]$ é simplesmente uma média populacional, podemos estimá-la com base na média amostral:

\displaystyle{\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]:=\frac{\sum_{i=1}^{n}{% \widehat{\mu}}(x,{\mathbf{Z}}_{i})}{n}\approx{\mathbb{E}}[{\widehat{\mu}}(x,{% \mathbf{Z}})]

Definição 3.25.

Considere que ${\mathbf{Z}}$ satisfaz a Definição 3.18 e ${\widehat{\mu}}(x,{\mathbf{z}})$ é uma estimativa da regressão ${\mathbb{E}}[Y|X=x,{\mathbf{Z}}={\mathbf{z}}]$ . Os estimadores de ${\mathbb{E}}[Y|do(X=x),{\mathbf{Z}}]$ e ${\mathbb{E}}[Y|do(X=x)]$ pela fórmula do ajuste são:

	$\displaystyle{\widehat{{\mathbb{E}}}}_{1}[Y\|do(X=x),{\mathbf{Z}}]$	$\displaystyle:={\widehat{\mu}}(x,{\mathbf{Z}})$
	$\displaystyle{\widehat{{\mathbb{E}}}}_{1}[Y\|do(X=x)]$	$\displaystyle:=\frac{\sum_{i=1}^{n}{\widehat{\mu}}(x,{\mathbf{Z}}_{i})}{n}$

A seguir mostraremos que, se ${\widehat{\mu}}$ converge para $\mu$ , então ${\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]$ converge para ${\mathbb{E}}[Y|do(X=x)]$ . Em outras palavras, é possível utilizar ${\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]$ para estimar o efeito causal de $X$ em $Y$ por meio de expressões como o ${ACE}$ .

Teorema 3.26.

Seja $\mu(X,{\mathbf{Z}}):={\mathbb{E}}[Y|X,{\mathbf{Z}}]$ . Se ${\mathbf{Z}}$ satisfaz a Definição 3.18, ${\mathbb{E}}[|\mu(x,{\mathbf{Z}}_{1})|]<\infty$ , ${\mathbb{E}}[|{\widehat{\mu}}(x,{\mathbf{Z}}_{1})-\mu(x,{\mathbf{Z}}_{1})|]=o(1)$ , e ${\widehat{\mu}}$ é invariante a permutações (Definição 3.23), então ${\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]\stackrel{{\scriptstyle{\mathbb{P}}}}{{% \longrightarrow}}{\mathbb{E}}[Y|do(X=x)]$ .

A seguir, utilizamos dados simulados para ilustrar a implementação da fórmula do ajuste.

Exemplo 3.27.

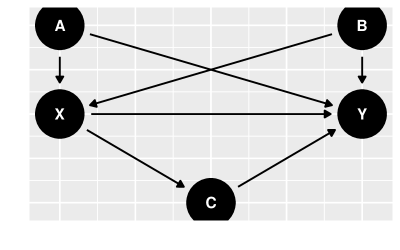
Considere que o grafo causal é dado pela figur 12. Vamos supor que os dados são gerados da seguinte forma: $\sigma^{2}=0.01$ , $A\sim N(0,\sigma^{2})$ , $B\sim N(0,\sigma^{2})$ , $\epsilon\sim Bernoulli(0.95)$ $X\equiv{\mathbb{I}}(A+B>0)\epsilon+{\mathbb{I}}(A+B<0)(1-\epsilon)$ , $C\sim N(X,\sigma^{2})$ , e $Y\sim N(A+B+C+X,\sigma^{2})$ :

\MakeFramed

# Especificar o grafo
grafo <- dagitty::dagitty("dag {
    X[e] Y[o]
    {A B} -> { X Y }; X -> {C Y}; C -> Y }")

# Simular os dados
n <- 10^5
sd = 0.1
A <- rnorm(n, 0, sd)
B <- rnorm(n, 0, sd)
eps <- rbinom(n, 1, 0.8)
X <- as.numeric(eps*((A + B) > 0) +
                  (1-eps)*((A + B) <= 0))
C <- rnorm(n, X, sd)
Y <- rnorm(n, A + B + C + X, sd)
data <- dplyr::tibble(A, B, C, X, Y)

\endMakeFramed

Estimaremos o efeito causal pela fórmula do ajuste (Definição 3.25). Iniciaremos a análise utilizando ${\widehat{\mu}}$ como sendo uma regressão linear simples:

\MakeFramed

# Sejam Z variáveis que satisfazem o critério backdoor para
# estimar o efeito causal de causa em efeito em grafo.
# Retorna uma fórmula do tipo Y ~ X + Z˙1 + … + Z˙d
fm_ajuste <- function(grafo, causa, efeito)
{
  var_backdoor <- dagitty::adjustmentSets(grafo)[[1]]
  regressores = c(causa, var_backdoor)
  fm = paste(regressores, collapse = "+")
  fm = paste(c(efeito, fm), collapse = "~")
  as.formula(fm)
}

# Estima E[Efeito—do(causa = x)] pela 
# formula do ajuste usando mu˙chapeu como regressao 
est_do_x_lm <- function(data, mu_chapeu, causa, x)
{
  data %>%
    dplyr::mutate({{causa}} := x) %>%
    predict(mu_chapeu, newdata = .) %>%
    mean()
}

# Estimação do ACE com regressão linear simples
fm <- fm˙ajuste(grafo, "X", "Y")
mu_chapeu_lm <- lm(fm, data = data)
ace_ajuste_lm = est˙do˙x˙lm(data, mu_chapeu_lm, "X", 1) -
  est˙do˙x˙lm(data, mu_chapeu_lm, "X", 0)
round(ace_ajuste_lm)

## [1] 2

\endMakeFramed

Em alguns casos, não é razoável supor que ${\mathbb{E}}[Y|X,{\mathbf{Z}}]$ é linear. Nestas situações, é fácil adaptar o código anterior para algum método não-paramétrico arbitrário. Exibimos uma implementação usando XGBoost (Chen2023):

\MakeFramed

library(xgboost)
var_backdoor <- dagitty::adjustmentSets(grafo, "X", "Y")[[1]]
mu_chapeu <- xgboost(
  data = data %>%
    dplyr::select(all˙of(c(var_backdoor, "X"))) %>%
    as.matrix(),
  label = data %>%
    dplyr::select(Y) %>%
    as.matrix(),
  nrounds = 100,
  objective = "reg:squarederror",
  early_stopping_rounds = 3,
  max_depth = 2,
  eta = .25,
  verbose = FALSE
)

est_do_x_xgb <- function(data, mu_chapeu, causa, x)
{
  data %>%
    dplyr::mutate({{causa}} := x) %>%
    dplyr::select(c(var_backdoor, causa)) %>%
    as.matrix() %>%
    predict(mu_chapeu, newdata = .) %>%
    mean()
}

ace_est_xgb = est˙do˙x˙xgb(data, mu_chapeu, "X", 1) -
  est˙do˙x˙xgb(data, mu_chapeu, "X", 0)
round(ace_est_xgb, 2)

## [1] 2

\endMakeFramed

Como o modelo linear era adequado para ${\mathbb{E}}[Y|X,{\mathbf{Z}}]$ , não vemos diferença entre a estimativa obtida pela regressão linear simples e pelo XGBoost. Mas será que as estimativas estão adequadas? Como simulamos os dados, é possível calcular diretamente ${\mathbb{E}}[Y|do(X=x)]$ :

$\displaystyle{\mathbb{E}}[Y\|do(X=x)]$	$\displaystyle={\mathbb{E}}[{\mathbb{E}}[Y\|X=x,A,B]]$
	$\displaystyle={\mathbb{E}}[{\mathbb{E}}[{\mathbb{E}}[Y\|X=x,A,B,C]\|X=x,A,B]]$	Lei da esperança total
	$\displaystyle={\mathbb{E}}[{\mathbb{E}}[A+B+C+X\|X=x,A,B]]$	$\displaystyle Y\sim N(A+B+C+X,\sigma^{2})$
	$\displaystyle={\mathbb{E}}[A+B+2x]$	$\displaystyle C\sim N(X,\sigma^{2})$
	$\displaystyle=2x$	$\displaystyle{\mathbb{E}}[A]={\mathbb{E}}[B]=0$	(6)

Uma vez calculado ${\mathbb{E}}[Y|do(X=x)]$ , podemos obter o ${ACE}$ :

	$\displaystyle{ACE}$	$\displaystyle={\mathbb{E}}[Y\|do(X=1)]-{\mathbb{E}}[Y\|do(X=0)]$
		$\displaystyle=2\cdot 1-2\cdot 0=2$

Portanto, as estimativas do ${ACE}$ obtidas pela regressão linear e pelo xgboost estão adequadas.

5.2.2 Ponderação pelo inverso do escore de propensidade (IPW)

Uma outra forma de estimar ${\mathbb{E}}[Y|do(X=x)]$ e ${\mathbb{E}}[Y|do(X=x),{\mathbf{Z}}]$ é motivada pelo Teorema 3.22. Este resultado determina que, se ${\mathbf{Z}}$ satisfaz a Definição 3.18, então

\displaystyle{\mathbb{E}}[Y|do(X=x),{\mathbf{Z}}]

\displaystyle=\frac{{\mathbb{E}}\left[Y{\mathbb{I}}(X=x)|{\mathbf{Z}}\right]}{% f(x|{\mathbf{Z}})}.

Na segunda expressão, ${\mathbb{E}}[Y{\mathbb{I}}(X=x)|{\mathbf{Z}}]$ é a regressão de $Y{\mathbb{I}}(X=x)$ em ${\mathbf{Z}}$ . Assim, esta quantidade pode ser estimada por um método de regressão arbitrário, que denotaremos por $\widehat{{\mathbb{E}}}[Y{\mathbb{I}}(X=x)|{\mathbf{Z}}]$ . Também $f(x|{\mathbf{z}})$ é usualmente chamado de escore de propensidade. Este escore captura a forma como os confundidores atuam sobre $X$ nos dados observacionais. Como $f$ em geral é desconhecido, $f(x|{\mathbf{z}})$ também o é. Contudo, quando $X$ é discreto, podemos estimar $f(x|{\mathbf{z}})$ utilizando algum algoritmo arbitrário de classificação. Denotaremos esta estimativa por $\widehat{f}(x|{\mathbf{z}})$ . Se a estimativa for boa, temos

\displaystyle{\mathbb{E}}[Y|do(X=x),{\mathbf{Z}}]

\displaystyle=\frac{\widehat{{\mathbb{E}}}[Y{\mathbb{I}}(X=x)|{\mathbf{Z}}]}{f% (x|{\mathbf{Z}})}\approx\frac{\widehat{{\mathbb{E}}}[Y{\mathbb{I}}(X=x)|{% \mathbf{Z}}]}{\widehat{f}(x|{\mathbf{z}})}.

O Teorema 3.22 também orienta a estimação de ${\mathbb{E}}[Y|do(X=x)]$ . Se ${\mathbf{Z}}$ satisfaz o critério backdoor, então

\displaystyle{\mathbb{E}}[Y|do(X=x)]

\displaystyle={\mathbb{E}}\left[\frac{Y{\mathbb{I}}(X=x)}{f(x|{\mathbf{Z}})}\right]

Como nesta expressão a esperança é uma média populacional, ela pode ser aproximada pela média amostral

\displaystyle{\mathbb{E}}\left[\frac{Y{\mathbb{I}}(X=x)}{f(x|{\mathbf{Z}})}\right]

\displaystyle\approx n^{-1}\sum_{i=1}^{n}\frac{Y_{i}{\mathbb{I}}(X_{i}=x)}{% \widehat{f}(x|{\mathbf{Z}}_{i})}.

Combinando estas aproximações, obtemos:

Definição 3.28.

Considere que ${\mathbf{Z}}$ satisfaz a Definição 3.18 e $\widehat{f}(x|{\mathbf{z}})$ é uma estimativa de $f(x|{\mathbf{z}})$ . Os estimadores de ${\mathbb{E}}[Y|do(X=x),{\mathbf{Z}}]$ e ${\mathbb{E}}[Y|do(X=x)]$ por IPW são:

	$\displaystyle{\widehat{{\mathbb{E}}}}_{2}[Y\|do(X=x),{\mathbf{Z}}]$	$\displaystyle:=\frac{\widehat{{\mathbb{E}}}[Y{\mathbb{I}}(X=x)\|{\mathbf{Z}}]}{% \widehat{f}(x\|{\mathbf{z}})}$
	$\displaystyle{\widehat{{\mathbb{E}}}}_{2}[Y\|do(X=x)]$	$\displaystyle:=n^{-1}\sum_{i=1}^{n}\frac{Y_{i}{\mathbb{I}}(X_{i}=x)}{\widehat{% f}(x\|{\mathbf{Z}}_{i})}.$

Se $\widehat{f}$ converge para $f$ , então sob condições relativamente pouco restritivas ${\widehat{{\mathbb{E}}}}_{2}[Y|do(X=x)]$ converge para ${\mathbb{E}}[Y|do(X=x)]$ .

Teorema 3.29.

Se ${\mathbf{Z}}$ satisfaz a Definição 3.18, também $\widehat{f}$ é invariante a permutações (Definição 3.23), ${\mathbb{E}}[|\widehat{f}(x|{\mathbf{Z}}_{1})-f(x|{\mathbf{Z}}_{1})|]=o(1)$ , e existe $M>0$ tal que $\sup_{\mathbf{z}}{\mathbb{E}}[|Y|{\mathbb{I}}(X=x)|{\mathbf{Z}}={\mathbf{z}}]<M$ , e existe $\delta>0$ tal que $\inf_{z}\min\{f(x|{\mathbf{Z}}_{1}),\widehat{f}(x|{\mathbf{Z}}_{1})\}>\delta$ , então ${\widehat{{\mathbb{E}}}}_{2}[Y|do(X=x)]\stackrel{{\scriptstyle{\mathbb{P}}}}{{% \longrightarrow}}{\mathbb{E}}[Y|do(X=x)]$ .

A seguir, utilizamos novamente dados simulados para ilustrar a implementação de IPW:

Exemplo 3.30.

Considere que o grafo causal e o modelo de geração dos dados são idênticos àqueles do Exemplo 3.27. Iniciaremos a análise utilizando regressão logística para estimar $\widehat{f}$ .

\MakeFramed

# Sejam Z variáveis que satisfazem o critério backdoor para
# estimar o efeito causal de causa em efeito em grafo.
# Retorna uma fórmula do tipo X ~ Z˙1 + … + Z˙d
fm_ipw <- function(grafo, causa, efeito)
{
 var_backdoor <- dagitty::adjustmentSets(grafo)[[1]]
 fm = paste(var_backdoor, collapse = "+")
 fm = paste(c(causa, fm), collapse = "~")
 as.formula(fm)
}

# Estimação do ACE por IPW onde
# Supomos X binário e
# f˙1 é o vetor P(X˙i=1—Z˙i)
ACE_ipw <- function(data, causa, efeito, f_1)
{
 data %>%
 mutate(f_1 = f_1,
        est_1 = {{efeito}}*({{causa}}==1)/f_1,
        est_0 = {{efeito}}*({{causa}}==0)/(1-f_1)
 ) %>%
 summarise(do_1 = mean(est_1),
           do_0 = mean(est_0)) %>%
 mutate(ACE = do_1 - do_0) %>%
 dplyr::select(ACE)
}

fm <- fm˙ipw(grafo, "X", "Y")
f_chapeu <- glm(fm, family = "binomial", data = data)
f_1_lm <- predict(f_chapeu, type = "response")
ace_ipw_lm <- data %>% ACE˙ipw(X, Y, f_1_lm) %>% as.numeric()
ace_ipw_lm %>% round(2)

## [1] 2.09

\endMakeFramed

Também é fácil adaptar o código acima para estimar ${ACE}$ por IPW utilizando algum método não-paramétrico para estimar $\widehat{f}$ . Abaixo há um exemplo utilizando o XGBoost:

\MakeFramed

var_backdoor <- dagitty::adjustmentSets(grafo)[[1]]
f_chapeu <- xgboost(
 data = data %>%
   dplyr::select(all˙of(var_backdoor)) %>%
   as.matrix(),
 label = data %>%
   dplyr::select(X) %>%
   as.matrix(),
 nrounds = 100,
 objective = "binary:logistic",
 early_stopping_rounds = 3,
 max_depth = 2,
 eta = .25,
 verbose = FALSE
)

covs <- data %>% dplyr::select(all˙of(var_backdoor)) %>% as.matrix()
f_1 <- predict(f_chapeu, newdata = covs)
data %>% ACE˙ipw(X, Y, f_1) %>% as.numeric() %>% round(2)

## [1] 1.97

\endMakeFramed

5.2.3 Estimador duplamente robusto

Os Teoremas 3.26 e 3.29 mostram que, sob suposições diferentes, ${\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]$ e ${\widehat{{\mathbb{E}}}}_{2}[Y|do(X=x)]$ convergem para ${\mathbb{E}}[Y|do(X=x)]$ . A ideia do estimador duplamente robusto é combinar ambos os estimadores de forma a garantir esta convergência sob suposições mais fracas. Para tal, a ideia por trás do estimador duplamente é que este convirja junto a ${\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]$ quando este é consistente e para ${\widehat{{\mathbb{E}}}}_{2}[Y|do(X=x)]$ quando aquele o é.

Definição 3.31.

Se ${\mathbf{Z}}$ satisfaz a Definição 3.18 e sejam $\widehat{f}$ e ${\widehat{\mu}}$ tais quais nas Definições 3.25 e 3.28. O estimador duplamente robusto para ${\mathbb{E}}[Y|do(X=x)]$ , ${\widehat{{\mathbb{E}}}}_{3}[Y|do(X=x)]$ é tal que

\displaystyle{\widehat{{\mathbb{E}}}}_{3}[Y|do(X=x)]

\displaystyle={\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]+{\widehat{{\mathbb{E}}}}% _{2}[Y|do(X=x)]-\sum_{i=1}^{n}\frac{{\mathbb{I}}(X_{i}=x){\widehat{\mu}}(x,{% \mathbf{Z}}_{i})}{n\hat{f}(x|{\mathbf{Z}}_{i})}

O estimador duplamente robusto é consistente para ${\mathbb{E}}[Y|do(X=x)]$ tanto sob as condições do Teorema 3.26 quanto sob as do Teorema 3.29. A ideia básica é que, sob as condições do Teorema 3.26, ${\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]$ é consistente para ${\mathbb{E}}[Y|do(X=x)]$ e ${\widehat{{\mathbb{E}}}}_{2}[Y|do(X=x)]-\sum_{i=1}^{n}\frac{{\mathbb{I}}(X_{i}% =x){\widehat{\mu}}(x,{\mathbf{Z}}_{i})}{n\hat{f}(x|{\mathbf{Z}}_{i})}$ converge para $0$ . Isto é, quando ${\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]$ é consistente, o estimador duplamente robusto seleciona este termo. Similarmente, sob as condições do Teorema 3.29, ${\widehat{{\mathbb{E}}}}_{2}[Y|do(X=x)]$ é consistente para ${\mathbb{E}}[Y|do(X=x)]$ e ${\widehat{{\mathbb{E}}}}_{1}[Y|do(X=x)]-\sum_{i=1}^{n}\frac{{\mathbb{I}}(X_{i}% =x){\widehat{\mu}}(x,{\mathbf{Z}}_{i})}{n\hat{f}(x|{\mathbf{Z}}_{i})}$ converge para $0$ .

Teorema 3.32.

Suponha que existe $\epsilon>0$ tal que $\inf_{\mathbf{z}}\widehat{f}(x|{\mathbf{z}})>\epsilon$ , existe $M>0$ tal que $\sup_{\mathbf{z}}{\widehat{\mu}}(x,{\mathbf{z}})<M$ , e ${\widehat{\mu}}$ e $\widehat{f}$ são invariantes a permutações (Definição 3.23). Se as condições do Teorema 3.26 ou do Teorema 3.29 estão satisfeitas, então

\displaystyle{\widehat{{\mathbb{E}}}}_{3}[Y|do(X=x)]\stackrel{{\scriptstyle{% \mathbb{P}}}}{{\longrightarrow}}{\mathbb{E}}[Y|do(X=x)].

Exemplo 3.33 (Estimador duplamente robusto).

Considere que o grafo causal e o modelo de geração dos dados são iguais àqueles descritos no Exemplo 3.27. Para implementar o estimador duplamente robusto combinaremos o estimador da fórmula do ajuste obtido por regressão linear no Exemplo 3.27 e aquele de IPW por regressão logística no Exemplo 3.30. \MakeFramed

mu_1_lm <- data %>%
  dplyr::mutate(X = 1) %>%
  predict(mu_chapeu_lm, newdata = .)
mu_0_lm <- data %>%
  dplyr::mutate(X = 0) %>%
  predict(mu_chapeu_lm, newdata = .)
corr <- data %>%
  mutate(mu_1 = mu_1_lm,
         mu_0 = mu_0_lm,
         f_1 = f_1_lm,
         corr_1 = (X == 1)*mu_1/f_1,
         corr_0 = (X == 0)*mu_0/(1-f_1)) %>%
  summarise(corr_1 = mean(corr_1),
            corr_0 = mean(corr_0)) %>%
  mutate(corr = corr_1 - corr_0) %>%
  dplyr::select(corr) %>%
  as.numeric()
ace_rob_lm <- ace_ajuste_lm + ace_ipw_lm - corr
ace_rob_lm %>% round(2)

## [1] 2

\endMakeFramed

5.3 Exercícios

Exercício 3.34.

Prove o Lema 3.16.

Exercício 3.35.

Prove o Lema 3.17.

Exercício 3.36.

Prove que se $X\notin Anc(Y)$ , então ${ACE}=0$ .

Exercício 3.37.

Prove que a variância amostral satisfaz o Definição 3.23.

Exercício 3.38.

Utilizando como referência o grafo e o código no Exemplo 3.27, simule dados tais que a estimativa do ${ACE}$ é diferente quando um método de regressão linear e um de regressão não-paramétrica são usados.

5.4 Regression Discontinuity Design (RDD)

Em determinadas situações, $X$ é completamente determinado pelos confundidores, ${\mathbf{Z}}$ (Lee2010). Por exemplo, considere que desejamos determinar o efeito causal que um determinado programa social do governo traz sobre o nível de educação dos cidadãos. Neste caso, $X$ é a indicadora de que o indíviduo é elegível ao programa e $Y$ mede o seu nível de educação. Em alguns casos, é razoável supor que $X$ é completamente determinado por $Z$ , a renda do indivíduo.

A situação acima traz desafios para a fórmula do ajuste e IPW discutidos anteriormente. Primeiramente, como $X=h({\mathbf{Z}})$ , não é possível estimar ${\mathbb{E}}[Y|X=x,{\mathbf{Z}}={\mathbf{z}}]$ quando $x\neq h({\mathbf{z}})$ . Portanto, não é possível utilizar a fórmula do ajuste, uma vez que ela se baseia na expressão ${\mathbb{E}}[{\mathbb{E}}[Y|X=x,{\mathbf{Z}}]]$ . Similarmente, o estimador de IPW envolve uma divisão por $f(x|{\mathbf{Z}})$ . Assim, quando $x\neq h({\mathbf{Z}})$ há uma divisão por $0$ , o que torna o estimador indefinido.

5.4.1 Identificação causal no RDD

Apesar destas dificuldades, é possível medir nestas situações parte do efeito causal de $X$ em $Y$ . Suponha que ${\mathbf{Z}}\in\Re$ e que existe $z_{1}$ tal que $X={\mathbb{I}}({\mathbf{Z}}\geq{\mathbf{z}}_{1})$ . Por exemplo, um benefício pode estar disponível apenas para cidadãos que tenham renda abaixo de um teto ou uma lei pode ter efeitos a partir de uma determinada data.

Neste caso, podemos estar interessados em ${\mathbb{E}}[Y|do(X=x),{\mathbf{Z}}={\mathbf{z}}_{1}]$ , o efeito causal que $X$ tem na fronteira de sua implementação. Intuitivamente, próximo a esta fronteira, as unidades amostrais são todas similares em relação aos confundidores. Assim, se na fronteira houver uma diferença em $Y$ entre os valores de $X$ , esta diferença deve ser decorrente do efeito causal de $X$ . Esta intuição é formalizada no resultado de identicação causal abaixo:

Teorema 3.39 (Hahn2001).

Considere que ${\mathbf{Z}}\in\Re$ satisfaz a Definição 3.18, $X\in\{0,1\}$ , e ${\mathbb{E}}[Y|do(X=0),{\mathbf{Z}}]$ e ${\mathbb{E}}[Y|do(X=1),{\mathbf{Z}}]$ são contínuas em ${\mathbf{Z}}={\mathbf{z}}_{1}$ .

Se $X\equiv{\mathbb{I}}({\mathbf{Z}}\geq{\mathbf{z}}_{1})$ , então

\displaystyle{CACE}({\mathbf{Z}}={\mathbf{z}}_{1})

\displaystyle=\lim_{{\mathbf{z}}\downarrow{\mathbf{z}}_{1}}{\mathbb{E}}[Y|{% \mathbf{Z}}={\mathbf{z}}]-\lim_{{\mathbf{z}}\uparrow{\mathbf{z}}_{1}}{\mathbb{% E}}[Y|{\mathbf{Z}}={\mathbf{z}}].

Se $f(x|{\mathbf{Z}})\in(0,1)$ é contínua exceto em ${\mathbf{z}}_{1}$ , então

\displaystyle{CACE}({\mathbf{Z}}={\mathbf{z}}_{1})

\displaystyle=\frac{\lim_{{\mathbf{z}}\downarrow{\mathbf{z}}_{1}}{\mathbb{E}}[% Y|{\mathbf{Z}}={\mathbf{z}}]-\lim_{{\mathbf{z}}\uparrow{\mathbf{z}}_{1}}{% \mathbb{E}}[Y|{\mathbf{Z}}={\mathbf{z}}]}{\lim_{{\mathbf{z}}\downarrow{\mathbf% {z}}_{1}}f(X=1|{\mathbf{Z}}={\mathbf{z}})-\lim_{{\mathbf{z}}\uparrow{\mathbf{z% }}_{1}}f(X=1|{\mathbf{Z}}={\mathbf{z}})}.

Um detalhe sutil do Teorema 3.39 é que $X\equiv{\mathbb{I}}({\mathbf{Z}}>{\mathbf{z}}_{1})$ não é o suficiente para termos certeza que ${\mathbf{Z}}$ satisfaz o critério backdoor. Por exemplo, considere que o governo criasse um benefício fiscal para todas empresas sediadas em um determinado município. Neste caso, a ocorrência do benefício é função da sede da empresa. Contudo, a relação causal é mais complexa. Se o benefício for suficientemente alto, poderia motivar empresas a moverem sua sede para o município. Em outras palavras, o benefício seria causa da localização da sede e não o contrário. Neste caso, não seria possível aplicar o Teorema 3.39. Este tipo de raciocínio indica que a análise por RDD é mais efetiva quando é difícil interferir sobre o valor de ${\mathbf{Z}}$ . Por exemplo, como um indivíduo não pode interferir sobre a sua idade, é mais fácil justificar o uso de RDD em uma campanha de vacinação em que apenas indivíduos acima de uma determinada idade são vacinados.

Um outro ponto importante de interpretação do Teorema 3.39 é que, embora ${\mathbb{E}}[Y|do(X=0),{\mathbf{Z}}]$ e ${\mathbb{E}}[Y|do(X=1),{\mathbf{Z}}]$ sejam supostas contínuas, $f(X=1|{\mathbf{Z}})$ e ${\mathbb{E}}[Y|{\mathbf{Z}}]$ não o são. Intuitivamente, podemos imaginar $X$ representa a indicadora de que uma determinada política é adotada. Por exemplo, podemos imaginar que $X$ indica que um indivíduo foi vacinado, ${\mathbf{Z}}$ a sua idade e $Y$ a sua hospitalização. Neste caso, ${\mathbb{E}}[Y|do(X=0),{\mathbf{Z}}]$ e ${\mathbb{E}}[Y|do(X=1),{\mathbf{Z}}]$ representam a taxa de hospitalização quando todos os indivíduos são vacinados ou quando todos eles não o são. Nestas situações, seria razoável supor que a taxa de hospitalização é contínua em função da idade, pois não esperamos que exista uma grande descontinuidade nas condições de saúde entre indivíduos com $69$ e com $70$ anos de idade. Este tipo de conclusão muitas vezes é resumido pela expressão em latim natura non facit saltus (a natureza não faz saltos). Por outro lado, nos dados observados, a política não é adotada para uma faixa de valores de ${\mathbf{Z}}$ e passa a ser adotada a partir de um ponto, o que é responsável pela descontinuidade em ${\mathbb{E}}[Y|{\mathbf{Z}}]$ e em $f(X=1|{\mathbf{Z}})$ . Podemos imaginar que a vacinação é empregada somente em indivíduos com mais de $70$ anos. Esta descontinuidade na política humana cria uma diferença importante entre indivíduos com $69$ e com $70$ anos, o que explica uma diferença grande nas taxas de hospitalização entre estas idades nos dados observados.

5.4.2 Estimação no RDD

O Teorema 3.39 indica que ${CACE}({\mathbf{Z}}={\mathbf{z}}_{1})$ é função da regressão de $Y$ sobre ${\mathbf{Z}}$ , ${\mathbb{E}}[Y|{\mathbf{Z}}]$ , e sobre o classificador, $f(X=1|{\mathbf{Z}})$ . Uma possível estratégia é estimarmos estas quantidades separadamente e, a seguir, estimarmos o ${CACE}$ trocando as quantias populacionais pelas quantias estimadas.

Uma dificuldade nesta estratégia é que sabemos que ${\mathbb{E}}[Y|{\mathbf{Z}}]$ e $f(X=1|{\mathbf{Z}})$ são discontínuas. Para lidar com esta dificuldade, uma possibilidade é realizar uma regressão para ${\mathbf{Z}}<{\mathbf{z}}_{1}$ e outra para ${\mathbf{Z}}\geq{\mathbf{z}}_{1}$ .

Definição 3.40.

Seja $D_{<}=\{i:{\mathbf{Z}}_{i}<{\mathbf{z}}_{1}\}$ o conjunto de unidades amostrais em que ${\mathbf{Z}}_{i}<{\mathbf{z}}_{1}$ , $\widehat{{\mathbb{E}}}_{<}[Y|{\mathbf{Z}}]$ e $\widehat{f}_{<}(X=1|{\mathbf{Z}})$ regressões ajustadas utilizando apenas dados em $D_{<}$ e $\widehat{{\mathbb{E}}}_{\geq}[Y|{\mathbf{Z}}]$ e $\widehat{f}_{\geq}(X=1|{\mathbf{Z}})$ ajustadas em $D^{c}_{<}$ . O estimador RDD para ${CACE}({\mathbf{z}}_{1})$ é

\displaystyle{\widehat{{CACE}}}({\mathbf{z}}_{1}):=\frac{\widehat{{\mathbb{E}}% }_{\geq}[Y|{\mathbf{z}}_{1}]-\widehat{{\mathbb{E}}}_{<}[Y|{\mathbf{z}}_{1}]}{% \widehat{f}_{\geq}(X=1|{\mathbf{Z}})-\widehat{f}_{<}(X=1|{\mathbf{Z}})}.

Em particular, se sabemos a priori que $f(X=1|{\mathbf{z}})=1$ para ${\mathbf{z}}\geq{\mathbf{z}}_{1}$ e $f(X=1|{\mathbf{z}})=0$ para ${\mathbf{z}}<{\mathbf{z}}_{1}$ , então

\displaystyle{\widehat{{CACE}}}({\mathbf{z}}_{1}):=\widehat{{\mathbb{E}}}_{% \geq}[Y|{\mathbf{z}}_{1}]-\widehat{{\mathbb{E}}}_{<}[Y|{\mathbf{z}}_{1}]

O exemplo a seguir ilustra a implementação de RDD quando $X\equiv{\mathbb{I}}({\mathbf{Z}}\geq{\mathbf{z}}_{1})$ utilizando tanto regressão linear quanto regressão de Kernel de Nadaraya-Watson.

Exemplo 3.41.

Considere que $Z_{i}$ satisfaz o critério backdoor para estimar o efeito causal de $X$ em $Y$ . Além disso, $Z_{i}\sim N(0,1)$ , $X_{i}\equiv{\mathbb{I}}(Z_{i}\geq 0)$ e $Y_{i}|X_{i},Z_{i}\sim N(50(X_{i}+1)(Z_{i}+1),1)$ . Podemos simular os dados da seguinte forma:

\MakeFramed

n <- 1000
Z <- rnorm(n)
X <- Z >= 0
Y <- rnorm(n, 50*(X+1)*(Z+1))
data <- tibble(X, Y, Z)
plot(Z, Y)

\endMakeFramed

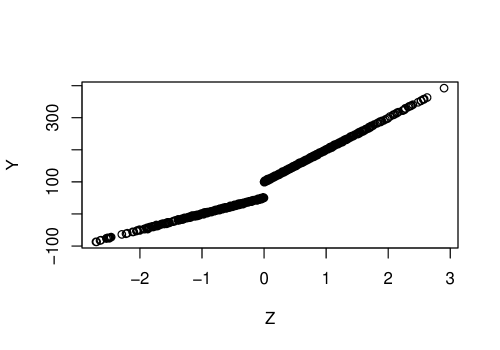
Como estamos simulando os dados, podemos calcular ${CACE}(0)$ :

	$\displaystyle{CACE}(0)$	$\displaystyle=\lim_{{\mathbf{z}}\downarrow 0}{\mathbb{E}}[Y\|{\mathbf{Z}}={% \mathbf{z}}]-\lim_{{\mathbf{z}}\uparrow 0}{\mathbb{E}}[Y\|{\mathbf{Z}}={\mathbf% {z}}]$
		$\displaystyle=\lim_{{\mathbf{z}}\downarrow 0}{\mathbb{E}}[Y\|X=1,{\mathbf{Z}}={% \mathbf{z}}]-\lim_{{\mathbf{z}}\uparrow 0}{\mathbb{E}}[Y\|X=0,{\mathbf{Z}}={% \mathbf{z}}]$
		$\displaystyle=\lim_{{\mathbf{z}}\downarrow 0}50(1+1)({\mathbf{z}}+1)-\lim_{{% \mathbf{z}}\uparrow 0}50(0+1)({\mathbf{z}}+1)=50$

O código abaixo estima ${CACE}(0)$ usando regressão linear:

\MakeFramed

regs = data %>%
  mutate(Z1 = (Z >= 0)) %>%
  group˙by(Z1) %>%
  summarise(
    intercepto = lm(Y ~ Z)$coefficients[1],
    coef_angular = lm(Y ~ Z)$coefficients[2]
  )
regs

## # A tibble: 2 x 3
##   Z1    intercepto coef_angular
##   <lgl>      <dbl>        <dbl>
## 1 FALSE       50.1         50.1
## 2 TRUE        99.9        100.

est_cace = 1*regs[2, 2] + 0*regs[2, 3] -
  1*regs[1, 2] + 0*regs[1, 3]
round(as.numeric(est_cace), 2)

## [1] 49.81

\endMakeFramed

Similarmente, podemos estimar ${CACE}(0)$ usando regressão por kernel de Nadaraya-Watson:

\MakeFramed

library(np)
options(np.messages = FALSE)
nw_reg <- function(data, valor)
{
  bw <- npregbw(xdat = data$Z, ydat = data$Y)$bw
  npksum(txdat= data$Z, exdat = valor, tydat = data$Y, bws = bw)$ksum/
    npksum(txdat = data$Z, exdat = valor, bws = bw)$ksum
}

reg_baixo <- data %>%
  filter(Z < 0) %>%
  nw˙reg(0)
reg_cima <- data %>%
  filter(Z >= 0) %>%
  nw˙reg(0)
est_cace <- reg_cima - reg_baixo
round(est_cace, 2)

## [1] 51.31

\endMakeFramed

5.5 Exercícios

Exercício 3.42.

Crie um exemplo em que, ao contrário do Exemplo 3.41, ${\mathbb{E}}[Y|X=1,{\mathbf{Z}}]$ não é linear em ${\mathbf{Z}}$ . Compare as estimativas de ${CACE}$ usando a regressão linear e algum método de regressão não-paramétrica.

	$\displaystyle f({\mathbf{z}}\|do(x))$	$\displaystyle=f({\mathbf{z}}),\text{ e }$
	$\displaystyle f(y\|do(x),{\mathbf{z}})$	$\displaystyle=f(y\|x,{\mathbf{z}}).$

	$\displaystyle{\mathbb{E}}[g(Y)\|do(X=x),{\mathbf{Z}}]$	$\displaystyle={\mathbb{E}}[g(Y)\|X=x,{\mathbf{Z}}],\text{ e }$
	$\displaystyle{\mathbb{E}}[g(Y)\|do(X=x)]$	$\displaystyle={\mathbb{E}}[{\mathbb{E}}[g(Y)\|X=x,{\mathbf{Z}}]]$

	$\displaystyle{\mathbb{E}}[g(Y)\|do(X=x),{\mathbf{Z}}]$	$\displaystyle=\frac{{\mathbb{E}}[g(Y){\mathbb{I}}(X=x)\|{\mathbf{Z}}]}{f(x\|{% \mathbf{Z}})},\text{ e }$
	$\displaystyle{\mathbb{E}}[g(Y)\|do(X=x)]$	$\displaystyle={\mathbb{E}}\left[\frac{g(Y){\mathbb{I}}(X=x)}{f(x\|{\mathbf{Z}})% }\right]$

	$\displaystyle{\widehat{{\mathbb{E}}}}_{2}[Y\|do(X=x),{\mathbf{Z}}]$	$\displaystyle:=\frac{\widehat{{\mathbb{E}}}[Y{\mathbb{I}}(X=x)\|{\mathbf{Z}}]}{% \widehat{f}(x\|{\mathbf{z}})}$
	$\displaystyle{\widehat{{\mathbb{E}}}}_{2}[Y\|do(X=x)]$	$\displaystyle:=n^{-1}\sum_{i=1}^{n}\frac{Y_{i}{\mathbb{I}}(X_{i}=x)}{\widehat{% f}(x\|{\mathbf{Z}}_{i})}.$