4 O modelo de probabilidade para intervenções

Com base no modelo estrutural causal discutido no capítulo 2, agora estabeleceremos um significado para o efeito causal de uma variável em outra.

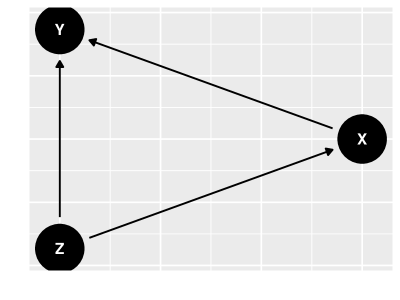
Refer to caption — Figura 7: Grafo que representa as relações causais entre Z (Sexo), X (Tratamento), e Y (Cura).

Para iniciar esta discussão, considere as variáveis $Z$ (Sexo), $X$ (Tratamento), e $Y$ (Cura), discutidas no capítulo 1. Podemos considerar que $Z$ é uma causa tanto de $X$ quanto de $Y$ e que $X$ é uma causa de $Y$ . Assim, podemos representar as relações causais entre estas variáveis por meio do grafo na figur 7. Usando este grafo, podemos discutir mais a fundo porque a probabilidade condicional de cura dado tratamento é distinta do efeito causal do tratamento na cura.

Quando calculamos a probabilidade condicional de cura dado o tratamento, estamos perguntando: “Qual é a probabilidade de que um indivíduo selecionado aleatoriamente da população se cure dado que aprendemos que recebeu o tratamento?” Para responder a esta pergunta, propagamos a informação do tratamento usado em todos os caminhos do tratamento para a cura. Assim, além do efeito direto que o tratamento tem na cura, o tratamento também está associado ao sexo do paciente, o que indiretamente traz mais informação sobre a cura deste. Isto é, neste caso o tratamento traz informação tanto sobre seus efeitos (cura), quanto sobre suas causas (sexo). Uma outra maneira de verificar estas afirmações é calculando diretamente $f(y|x)$ :

$\displaystyle f(y\|x)$	$\displaystyle=\sum_{s}f(z,y\|x)$
	$\displaystyle=\sum_{s}\frac{f(z,y,x)}{f(x)}$
	$\displaystyle=\sum_{s}\frac{f(z,x)f(y\|z,x)}{f(x)}$
	$\displaystyle=\sum_{s}f(z\|x)f(y\|z,x)$	(2)

Notamos na Seção 4 que $f(y|x)$ é a média das probabilidades de cura em cada sexo, $f(y|z,x)$ , ponderadas pela distribuição do sexo após aprender o tratamento do indivíduo, $f(z|x)$ .

A probabilidade condicional de cura dado tratamento não corresponde àquilo que entendemos por efeito causal de tratamento em cura. Este efeito é a resposta para a pergunta: “Qual a probabilidade de que um indivíduo selecionado aleatoriamente da população se cure dado que prescrevemos a ele o tratamento?”. Ao contrário da primeira pergunta, em que apenas observamos a população, nesta segunda fazemos uma intervenção sobre o comportamento do indivíduo. Assim, estamos fazendo uma pergunta sobre uma distribuição de probabilidade diferente, em que estamos agindo sobre a unidade amostral. Por exemplo, suponha que prescreveríamos o tratamento a qualquer indivíduo que fosse amostrado. Neste caso, saber qual tratamento foi aplicado não traria qualquer informação sobre o sexo do indivíduo. Em outras palavras, se chamarmos $f(y|do(x))$ como a probabilidade de cura dado que fazemos uma intervenção no tratamento, faria sentido obtermos:

\displaystyle f(y|do(x))

\displaystyle=\sum_{s}f(z)f(y|z,x)

(3)

Na likning 3 temos que o efeito causal do tratamento na cura é a média ponderada das probabilidades de cura em cada sexo ponderada pelas probabilidades de sexo de um indivíduo retirado aleatoriamente da população. Isto é, ao contrário da Seção 4, a distribuição do sexo do indivíduo não é alterada quando fazemos uma intervenção sobre o tratamento.

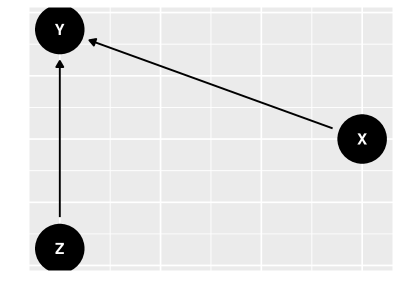
Com base neste exemplo, podemos generalizar o que entendemos por intervenção. Quando fazemos uma intervenção em uma variável, $V_{1}$ , tomamos uma ação para que $V_{1}$ assuma um determinado valor. Assim, as demais variáveis que comumente seriam causas de $V_{1}$ deixam de sê-lo. Por exemplo, para o caso na figur 7, o modelo de intervenção removeria a aresta de Sexo para Tratamento, resultado na figur 8.

Com base nas observações acima, finalmente podemos definir o modelo de probabilidade sob intervenção:

Definição 3.1.

Seja ${\mathcal{G}}=({\mathcal{V}},{\mathcal{E}})$ um DAG, $({\mathcal{G}},f)$ um CM (Definição 2.24), e ${\mathbb{V}}_{1}\subseteq{\mathcal{V}}$ . O modelo de probabilidade obtido após uma intervenção em ${\mathbb{V}}_{1}$ é dado por:

	$\displaystyle f({\mathcal{V}}\|do({\mathbb{V}}_{1}))$	$\displaystyle:=\prod_{V_{2}\in{\mathbb{V}}_{2}}f(V_{2}\|Pa(V_{2}))$	, ou equivalentemente
	$\displaystyle f({\mathcal{V}}\|do({\mathbb{V}}_{1}={\mathbf{v}}_{1}))$	$\displaystyle:=\left(\prod_{(v_{1},V_{1})\in({\mathbf{v}}_{1},{\mathbb{V}}_{1}% )}{\mathbb{I}}(V_{1}=v_{1})\right)\cdot\left(\prod_{V_{2}\notin{\mathbb{V}}_{1% }}f(V_{2}\|Pa(V_{2}))\right)$

Para compreender a Definição 3.1, podemos comparar o modelo de intervenção com o modelo observacional:

\displaystyle f({\mathbb{V}}_{2}|{\mathbb{V}}_{1})

\displaystyle\propto f({\mathbb{V}}_{1},{\mathbb{V}}_{2})=\left(\prod_{V_{1}% \in{\mathbb{V}}_{1}}f(V_{1}|Pa(V_{1})\right)\cdot\left(\prod_{V_{2}\in{\mathbb% {V}}_{2}}f(V_{2}|Pa(V_{2})\right)

No modelo observacional, a densidade de ${\mathbb{V}}_{2}$ dado ${\mathbb{V}}_{1}$ é proporcional ao produto, para todos os vértices, da densidade do vértice dadas suas causas. Ao contrário, no modelo de intervenção supomos que os vértices em ${\mathbb{V}}_{1}$ são pré-fixados e, assim, não são gerados por suas causas usuais. Assim, na Definição 3.1, a densidade de ${\mathbb{V}}_{2}$ dada uma intervenção em ${\mathbb{V}}_{1}$ é dada o produto somente nos vértices de ${\mathbb{V}}_{2}$ das densidades do vértice dadas suas causas.

Esta análise é formalizada no Lema 3.2:

Lema 3.2.

Seja ${\mathcal{G}}(\bar{{\mathbf{X}}})$ o grafo obtido retirando-se de ${\mathcal{G}}$ todas as arestas que apontam para algum vértice em ${\mathbf{X}}$ . A densidade $f^{*}\equiv f({\mathcal{V}}|do({\mathbf{X}}={\mathbf{x}}))$ é compatível com ${\mathcal{G}}(\bar{{\mathbf{X}}})$ . Além disso, ${\mathbf{X}}$ é degenerada em ${\mathbf{x}}$ segundo $f^{*}$ .

Com base na discussão acima, podemos definir o efeito causal que um conjunto de variáveis, ${\mathbf{X}}$ , tem em outro conjunto, ${\mathbf{Y}}$ :

Definição 3.3.

${\mathbb{E}}[{\mathbf{Y}}|do({\mathbf{X}})]:=\int{\mathbf{y}}\cdot f({\mathbf{% y}}|do({\mathbf{X}}))d{\mathbf{y}}$ .

Definição 3.4.

O efeito causal médio, ACE_X,Y,¹¹ 1 A sigla ACE tem como origem a expressão em inglês, Average Causal Effect. Optamos por manter a sigla sem tradução para facilitar a comparação com artigos da área. Em outros contextos, este termo também é chamado de Average Treatment Effect e recebe o acrônimo ATE. de $X\in\Re$ em $Y\in\Re$ é dado por:

\displaystyle{ACE}_{X,Y}

\displaystyle=\begin{cases}{\mathbb{E}}[Y|do(X=1)]-{\mathbb{E}}[Y|do(X=0)]&% \text{, se $X$ é binário},\\ \frac{d{\mathbb{E}}[Y|do(X=x)]}{dx}&\text{, se $X$ é contínuo}.\end{cases}

Quando não há ambiguidade, escrevemos simplesmente ${ACE}$ ao invés de ${ACE}_{X,Y}$ .

Com a Definição 3.4 podemos finalmente desvendar o Paradoxo de Simpson discutido no capítulo 1. Veremos que o método que desenvolvemos resolve a questão com simplicidade, assim trazendo clareza ao Paradoxo.

Exemplo 3.5.

Considere que $(X,Y,Z)\in\Re^{3}$ são tais que $X$ e $Y$ são as indicadores de que, respectivamente, o paciente recebeu o tratamento e se curou. Além disso, suponha que a distribuição conjunta de $(X,Y,Z)$ é dada pelas frequências na tabela 1. Isto é:

	$\displaystyle{\mathbb{P}}(Z=1)=\frac{25+55+71+192}{700}\approx 0.49$
	$\displaystyle{\mathbb{P}}(Z=0)=1-{\mathbb{P}}(Z=1)\approx 0.51$
	$\displaystyle{\mathbb{P}}(Z=1\|X=0)=\frac{25+55}{25+55+36+234}\approx 0.23$
	$\displaystyle{\mathbb{P}}(Z=1\|X=1)=\frac{71+192}{71+192+6+81}\approx 0.75$
	$\displaystyle{\mathbb{P}}(Y=1\|X=0,Z=0)=\frac{234}{234+36}\approx 0.87$
	$\displaystyle{\mathbb{P}}(Y=1\|X=1,Z=0)=\frac{81}{81+6}\approx 0.93$
	$\displaystyle{\mathbb{P}}(Y=1\|X=0,Z=1)=\frac{55}{25+55}\approx 0.69$
	$\displaystyle{\mathbb{P}}(Y=1\|X=1,Z=1)=\frac{192}{71+192}\approx 0.73$

Agora, veremos que a probabilidade de $Y$ dada uma intervenção em $X$ depende do DAG usado no modelo causal estrutural.

Suponha que $Z$ é a indicadora de que o sexo do paciente é masculino. Neste caso, utilizaremos como grafo causal aquele em figur 7. este grafo, obtemos:

\displaystyle{\mathbb{P}}_{1}(Y=i,Z=j|do(X=k))

\displaystyle={\mathbb{P}}(Z=j){\mathbb{P}}(Y=i|X=k,Z=j)

(4)

Assim,

	$\displaystyle{\mathbb{P}}_{1}(Y=1\|do(X=1))$	$\displaystyle={\mathbb{P}}_{1}(Y=1,Z=0\|do(X=1))+{\mathbb{P}}_{1}(Y=1,Z=1\|do(X=% 1))$
		$\displaystyle={\mathbb{P}}(Z=0){\mathbb{P}}(Y=1\|X=1,Z=0)+{\mathbb{P}}(Z=1){% \mathbb{P}}(Y=1\|X=1,Z=1)$
		$\displaystyle\approx 0.51\cdot 0.93+0.49\cdot 0.73\approx 0.83$
	$\displaystyle{\mathbb{P}}_{1}(Y=1\|do(X=0))$	$\displaystyle={\mathbb{P}}_{1}(Y=1,Z=0\|do(X=0))+{\mathbb{P}}_{1}(Y=1,Z=1\|do(X=% 0))$
		$\displaystyle={\mathbb{P}}(Z=0){\mathbb{P}}(Y=1\|X=0,Z=0)+{\mathbb{P}}(Z=1){% \mathbb{P}}(Y=1\|X=0,Z=1)$
		$\displaystyle\approx 0.51\cdot 0.87+0.49\cdot 0.69\approx 0.78$

Portanto, o efeito causal do tratamento na cura quando $Z$ é o sexo do paciente é obtido abaixo:

	$\displaystyle{ACE}_{1}$	$\displaystyle={\mathbb{E}}_{1}[Y\|do(X=1)]-{\mathbb{E}}_{1}[Y\|do(X=0)]$
		$\displaystyle={\mathbb{P}}_{1}(Y=1\|do(X=1))-{\mathbb{P}}_{1}(Y=1\|do(X=0))% \approx 0.05$

Como esperado da discussão na Seção 1, o tratamento tem efeito causal médio positivo, isto é, ele aumenta a probabilidade de cura do paciente.

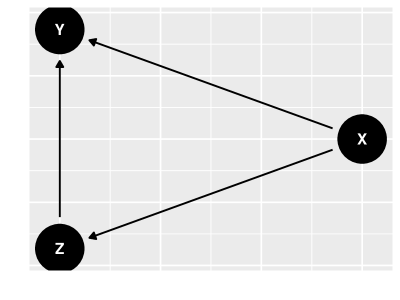
A seguir, consideramos que $Z$ é a indicadora de pressão sanguínea elevada do paciente. Assim, tomamos o grafo causal como aquele na figur 9. Utilizando este grafo, obtemos:

\displaystyle{\mathbb{P}}_{2}(Y=i,Z=j|do(X=k))

\displaystyle={\mathbb{P}}(Z=j|X=k){\mathbb{P}}_{1}(Y=i|X=k,Z=j)

(5)

Assim,

	$\displaystyle{\mathbb{P}}_{2}(Y=1\|do(X=1))$	$\displaystyle={\mathbb{P}}_{2}(Y=1,Z=0\|do(X=1))+{\mathbb{P}}_{2}(Y=1,Z=1\|do(X=% 1))$
		$\displaystyle={\mathbb{P}}(Z=0\|X=1){\mathbb{P}}(Y=1\|X=1,Z=0)+{\mathbb{P}}(Z=1\|% X=1){\mathbb{P}}(Y=1\|X=1,Z=1)$
		$\displaystyle\approx 0.25\cdot 0.93+0.75\cdot 0.73\approx 0.78$
	$\displaystyle{\mathbb{P}}_{2}(Y=1\|do(X=0))$	$\displaystyle={\mathbb{P}}_{2}(Y=1,Z=0\|do(X=0))+{\mathbb{P}}_{2}(Y=1,Z=1\|do(X=% 0))$
		$\displaystyle={\mathbb{P}}(Z=0\|X=0){\mathbb{P}}(Y=1\|X=0,Z=0)+{\mathbb{P}}(Z=1\|% X=0){\mathbb{P}}(Y=1\|X=0,Z=1)$
		$\displaystyle\approx 0.77\cdot 0.87+0.23\cdot 0.69\approx 0.83$

Portanto, o efeito causal do tratamento na cura quando $Z$ é a pressão sanguínea do paciente é obtido abaixo:

	$\displaystyle{ACE}_{1}$	$\displaystyle={\mathbb{E}}_{2}[Y\|do(X=1)]-{\mathbb{E}}_{2}[Y\|do(X=0)]$
		$\displaystyle={\mathbb{P}}_{2}(Y=1\|do(X=1))-{\mathbb{P}}_{2}(Y=1\|do(X=0))% \approx-0.05$

Como esperado da discussão na Seção 1, o tratamento tem efeito causal médio negativo, isto é, ele tem como efeito colateral grave a elevação da pressão sanguínea do paciente, reduzindo a probabilidade de cura deste.

Comparando as expressões obtidas em ${ACE}_{1}$ e ${ACE}_{2}$ , verificamos que o grafo causal desempenha papel fundamental na determinação do modelo de probabilidade sob intervenção. Ademais, o uso do grafo causal adequado em cada situação formaliza a discussão qualitativa desenvolvida na Seção 1. Não há paradoxo!

Se $({\mathcal{G}},f)$ é um CM linear Gaussiano, então é possível obter uma equação direta para o ${ACE}$ . Este resultado é apresentado no Teorema 3.6 abaixo.

Teorema 3.6.

Se $({\mathcal{G}},f)$ é um CM linear Gaussiano de parâmetros $\mu$ e $\beta$ e $\mathbb{C}_{X,Y}$ é o conjunto de todos os caminhos direcionados de $X$ a $Y$ , então

\displaystyle{ACE}_{X,Y}

\displaystyle=\sum_{C\in\mathbb{C}_{X,Y}}\prod_{i=1}^{|C|-1}\beta_{C_{i+1},C_{% i}}.

O Teorema 3.6 indica um algoritmo para calcular o ${ACE}_{X,Y}$ em um CM linear Gaussiano. Primeiramente, para cada caminho direcionado de $X$ em $Y$ calcula-se o produto dos coeficientes de regressão ligados a este caminho. Se imaginarmos os vértices no meio do caminho como mediadores, então estamos combinando o efeito de $X$ em $C_{2}$ , de $C_{2}$ em $C_{3}$ …e de $C_{m-1}$ em $Y$ para obter o efeito total de $X$ em $Y$ por este caminho. Ao final, somamos os efeitos totais obtidos por todos os caminhos. Cada caminho direcionado indica uma forma em que $X$ pode ter efeito sobre $Y$ . Ao levarmos todoas as formas em consideração, obtemos o efeito causal médio.

Além do efeito causal médio, às vezes desejamos determinar o efeito causal de $X$ em $Y$ quando observamos que a unidade amostral faz parte de determinado estrato da população. Em outras palavras, desejamos saber o efeito causal de $X$ em $Y$ quando observamos que outras variáveis, ${\mathbf{Z}}$ , assumem um determinado valor.

Definição 3.7.

O efeito causal médio condicional, CACE, de $X\in\Re$ em $Y\in\Re$ dado ${\mathbf{Z}}$ é:

\displaystyle{CACE}({\mathbf{Z}})

\displaystyle=\begin{cases}{\mathbb{E}}[Y|do(X=1),{\mathbf{Z}}]-{\mathbb{E}}[Y% |do(X=0),{\mathbf{Z}}]&\text{, se $X$ é binário},\\ \frac{d{\mathbb{E}}[Y|do(X=x),{\mathbf{Z}}]}{dx}&\text{, se $X$ é contínuo}.% \end{cases}

Uma vez estabelecido o modelo de probabilidade utilizado quando estudamos intervenções, agora podemos fazer inferência sobre o efeito causal. Para realizar tal inferência, em geral teremos de abordar duas questões:

1.

Identificação causal: Temos acesso a dados que são gerados segundo a distribuição observacional. Como é possível determinar o efeito causal em termos da distribuição observacional?
2.

Estimação: Uma vez estabelecida uma ligação entre a distribuição observacional dos dados e o efeito causal, como é possível estimá-lo?

Nas próximas seções estudaremos algumas estratégias gerais para a resolução destas questões. Consideraremos que desejamos medir o efeito causal de $X$ em $Y$ , onde $X,Y\in{\mathcal{V}}$ .

4.1 Exercícios

Exercício 3.8.

Considere que $X_{1}$ e $X_{2}$ são variáveis binárias. Também considere as seguintes definições: ACE := ${\mathbb{P}}(X_{2}=1|do(X_{1}=1))-{\mathbb{P}}(X_{2}=1|do(X_{1}=0))$ , e RD := ${\mathbb{P}}(X_{2}=1|X_{1}=1)-{\mathbb{P}}(X_{2}=1|X_{1}=0)$ . Explique em palavras a diferença entre ACE e RD e apresente um exemplo em que essa diferença ocorre.

Exercício 3.9 (Glymour2016[p.32]).

$(X_{1},X_{2},X_{3},X_{4})$ são variáveis binárias tais que $X_{i-1}$ é a única causa imediata de $X_{i}$ . Além disso, ${\mathbb{P}}(X_{1}=1)=0.5$ , ${\mathbb{P}}(X_{i}=1|X_{i-1}=1)=p_{11}$ e ${\mathbb{P}}(X_{i}=1|X_{i-1}=0)=p_{01}$ . Calcule:

(a)

${\mathbb{P}}(X_{1}=1,X_{2}=0,X_{3}=1,X_{4}=0)$ ,
(b)

${\mathbb{P}}(X_{4}=1|X_{1}=1)$ , ${\mathbb{P}}(X_{4}=1|do(X_{1}=1)$ ,
(c)

${\mathbb{P}}(X_{1}=1|X_{4}=1)$ , ${\mathbb{P}}(X_{1}=1|do(X_{4}=1)$ , e
(d)

${\mathbb{P}}(X_{3}=1|X_{1}=0,X_{4}=1)$

Exercício 3.10 (Glymour2016[p.29]).

Considere que $(U_{1},U_{2},U_{3})$ são independentes e tais que $U_{i}\sim N(0,1)$ . Também, $X_{1}\equiv U_{1}$ , $X_{2}\equiv 3^{-1}X_{1}+U_{2}$ , e $X_{3}\equiv 2^{-4}X_{2}+U_{3}$ . Considere que $X_{1}$ é a causa imediata de $X_{2}$ , que por sua vez é a causa imediata de $X_{3}$ . Além disso, cada $U_{i}$ influencia diretamente somente $X_{i}$ .

(a)

Desenhe o DAG que representa a estrutura causal indicada no enunciado.
(b)

Calcule ${\mathbb{E}}[X_{2}|X_{1}=3]$ e ${\mathbb{E}}[X_{2}|do(X_{1}=3)]$ .
(c)

Calcule ${\mathbb{E}}[X_{3}|X_{1}=6]$ e ${\mathbb{E}}[X_{3}|do(X_{1}=6)]$ .
(d)

Calcule ${\mathbb{E}}[X_{1}|X_{2}=1]$ e ${\mathbb{E}}[X_{1}|do(X_{2}=1)]$ .
(e)

Calcule ${\mathbb{E}}[X_{2}|X_{1}=1,X_{3}=3]$ , ${\mathbb{E}}[X_{2}|X_{1}=1,do(X_{3}=3)]$ , e ${\mathbb{E}}[X_{2}|do(X_{1}=1),X_{3}=3]$ .

$\displaystyle f(y\|x)$	$\displaystyle=\sum_{s}f(z,y\|x)$
	$\displaystyle=\sum_{s}\frac{f(z,y,x)}{f(x)}$
	$\displaystyle=\sum_{s}\frac{f(z,x)f(y\|z,x)}{f(x)}$
	$\displaystyle=\sum_{s}f(z\|x)f(y\|z,x)$	(2)

	$\displaystyle f({\mathcal{V}}\|do({\mathbb{V}}_{1}))$	$\displaystyle:=\prod_{V_{2}\in{\mathbb{V}}_{2}}f(V_{2}\|Pa(V_{2}))$	, ou equivalentemente
	$\displaystyle f({\mathcal{V}}\|do({\mathbb{V}}_{1}={\mathbf{v}}_{1}))$	$\displaystyle:=\left(\prod_{(v_{1},V_{1})\in({\mathbf{v}}_{1},{\mathbb{V}}_{1}% )}{\mathbb{I}}(V_{1}=v_{1})\right)\cdot\left(\prod_{V_{2}\notin{\mathbb{V}}_{1% }}f(V_{2}\|Pa(V_{2}))\right)$

	$\displaystyle{\mathbb{P}}(Z=1)=\frac{25+55+71+192}{700}\approx 0.49$
	$\displaystyle{\mathbb{P}}(Z=0)=1-{\mathbb{P}}(Z=1)\approx 0.51$
	$\displaystyle{\mathbb{P}}(Z=1\|X=0)=\frac{25+55}{25+55+36+234}\approx 0.23$
	$\displaystyle{\mathbb{P}}(Z=1\|X=1)=\frac{71+192}{71+192+6+81}\approx 0.75$
	$\displaystyle{\mathbb{P}}(Y=1\|X=0,Z=0)=\frac{234}{234+36}\approx 0.87$
	$\displaystyle{\mathbb{P}}(Y=1\|X=1,Z=0)=\frac{81}{81+6}\approx 0.93$
	$\displaystyle{\mathbb{P}}(Y=1\|X=0,Z=1)=\frac{55}{25+55}\approx 0.69$
	$\displaystyle{\mathbb{P}}(Y=1\|X=1,Z=1)=\frac{192}{71+192}\approx 0.73$

	$\displaystyle{\mathbb{P}}_{1}(Y=1\|do(X=1))$	$\displaystyle={\mathbb{P}}_{1}(Y=1,Z=0\|do(X=1))+{\mathbb{P}}_{1}(Y=1,Z=1\|do(X=% 1))$
		$\displaystyle={\mathbb{P}}(Z=0){\mathbb{P}}(Y=1\|X=1,Z=0)+{\mathbb{P}}(Z=1){% \mathbb{P}}(Y=1\|X=1,Z=1)$
		$\displaystyle\approx 0.51\cdot 0.93+0.49\cdot 0.73\approx 0.83$
	$\displaystyle{\mathbb{P}}_{1}(Y=1\|do(X=0))$	$\displaystyle={\mathbb{P}}_{1}(Y=1,Z=0\|do(X=0))+{\mathbb{P}}_{1}(Y=1,Z=1\|do(X=% 0))$
		$\displaystyle={\mathbb{P}}(Z=0){\mathbb{P}}(Y=1\|X=0,Z=0)+{\mathbb{P}}(Z=1){% \mathbb{P}}(Y=1\|X=0,Z=1)$
		$\displaystyle\approx 0.51\cdot 0.87+0.49\cdot 0.69\approx 0.78$

	$\displaystyle{\mathbb{P}}_{2}(Y=1\|do(X=1))$	$\displaystyle={\mathbb{P}}_{2}(Y=1,Z=0\|do(X=1))+{\mathbb{P}}_{2}(Y=1,Z=1\|do(X=% 1))$
		$\displaystyle={\mathbb{P}}(Z=0\|X=1){\mathbb{P}}(Y=1\|X=1,Z=0)+{\mathbb{P}}(Z=1\|% X=1){\mathbb{P}}(Y=1\|X=1,Z=1)$
		$\displaystyle\approx 0.25\cdot 0.93+0.75\cdot 0.73\approx 0.78$
	$\displaystyle{\mathbb{P}}_{2}(Y=1\|do(X=0))$	$\displaystyle={\mathbb{P}}_{2}(Y=1,Z=0\|do(X=0))+{\mathbb{P}}_{2}(Y=1,Z=1\|do(X=% 0))$
		$\displaystyle={\mathbb{P}}(Z=0\|X=0){\mathbb{P}}(Y=1\|X=0,Z=0)+{\mathbb{P}}(Z=1\|% X=0){\mathbb{P}}(Y=1\|X=0,Z=1)$
		$\displaystyle\approx 0.77\cdot 0.87+0.23\cdot 0.69\approx 0.83$