6 Controlando mediadores (critério frontdoor)

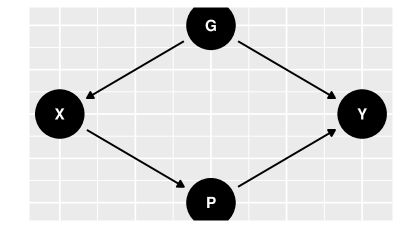
Há casos em que não existem variáveis observadas que satisfazem o critério backdoor. Por exemplo, considere o grafo causal na figur 14 (Glymour2016). Neste grafo, estamos interessados em compreender o efeito causal do fumo ($X$) sobre a incidência de câncer ($Y$). Além disso, fatores genéticos não observáveis ($G$) são um potencial confundidor, uma vez que podem ter influência tanto sobre o fumo quanto sobre a incidência de câncer. Assim, como $G$ não é observado, não é possível implementar os métodos de estimação vistos na última seção. Apesar desta dificuldade, ainda é possível medir o efeito causal de $X$ em $Y$ na figur 14.

Para tal, primeiramente observe que é possível estimar o efeito causal de $X$ em $P$ e de $P$ em $Y$. Para medir o efeito causal de $X$ em $P$, note que $\emptyset$ satisfaz o critério backdoor. Isso ocorre pois $Y$ é um colisor em $X\leftarrow G\rightarrow Y\leftarrow P$. Além disso, como $X=Pa(P)$, decorre do Lema 3.17 que $X$ satisfaz o critério backdoor para medir o efeito causal de $P$ em $Y$. Das duas últimas conclusões decorre do Teorema 3.19 que $f(P|do(X))=f(P|X)$ e que $f(Y|do(P))=\int f(Y|P,X)f(X)dX$.

A seguir, o critério frontdoor consiste em observar que $P$ está no único caminho direcionado de $X$ a $Y$, $X\rightarrow P\rightarrow Y$. Assim, é possível provar a identificação causal

O critério frontdoor é formalizado a seguir:

A Definição 3.43 elenca todos os itens que utilizamos na análise da figur 14. O primeiro item do critério identifica que ${\mathbf{W}}$ deve interceptar todos os caminhos direcionados de $X$ a $Y$. Isto é, ${\mathbf{W}}$ capturar a informação de todos os mediadores de $X$ a $Y$. O segundo e terceiro itens estabelecem as condições para que seja possível aplicar o critério backdoor para identificar $f({\mathbf{W}}|do(X))$ e $f(Y|do({\mathbf{W}}))$.