12 Teorema do Limite Central

Teorema 12.1 (Teorema do Limite Central).

Sejam X1,X2,X3,…X_{1},X_{2},X_{3},\dots variáveis aleatórias independentes entre si, quadrado-integráveis, com a mesma distribuição. Denote sua média por μ\mu e variância por σ2>0\sigma^{2}>0. Então, para todo a<ba<b

ℙ⁢(a⩽X1+⋯+Xn−n⋅μσ⋅n⩽b)≈∫ab12⁢π⁢e−x2/2⁢dx.\mathbb{P}\Big{(}a\leqslant\frac{X_{1}+\dots+X_{n}-n\cdot\mu}{\sigma\cdot\sqrt% {n}}\leqslant b\Big{)}\approx\int_{a}^{b}\tfrac{1}{\sqrt{2\pi}}e^{-x^{2}/2}\,% \mathrm{d}x.

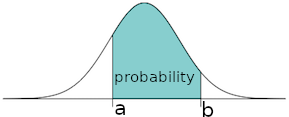
A aproximação “≈{\approx}” significa que a probabilidade se aproxima o quanto desejarmos da integral (como mostrado na Figura 12.1) se escolhermos nn suficientemente grande.

Esse fenômeno notável está no cerne da estatística e da maioria das ciências naturais. Ele afirma que, independentemente da distribuição de XX, se adicionarmos um número suficiente de amostras de XX, só veremos sua média μ\mu e variância σ2\sigma^{2}.

Refer to caption
Figura 12.1: Gráfico de y=12⁢π⁢e−x2/2y=\frac{1}{\sqrt{2\pi}}e^{-x^{2}/2} e a probabilidade de que Z∈[a,b]Z\in[a,b] representada pela área esverdeada entre os pontos aa e bb.

Não demonstraremos o Teorema do Limite Central neste módulo, pois são necessárias ferramentas mais avançadas.

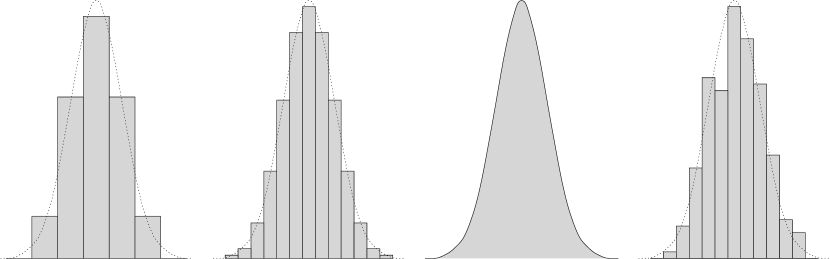
No caso de X∼Bernoulli⁢(12)X\sim\mathrm{Bernoulli}(\frac{1}{2}), o que corresponde a lançar uma moeda justa, podemos visualizar como a distribuição de X1+⋯+XnX_{1}+\dots+X_{n} se aproxima da função y=12⁢π⁢e−x2/2y=\frac{1}{\sqrt{2\pi}}e^{-x^{2}/2}, como ilustrado na Figura 12.2.

Exemplo 12.2.

Ao contar os votos em uma eleição muito disputada, 25.301 votos já foram contados: 12.636 para o Candidato A e 12.665 para o Candidato B. Ainda faltam 400 votos para serem contados. Qual é a probabilidade de que o Candidato B vença a eleição?

Supondo que cada voto seja como uma moeda justa, a pergunta que estamos fazendo é:

ℙ⁢(X1+⋯+X400⩾215)\mathbb{P}(X_{1}+\dots+X_{400}\geqslant 215)

onde X1,…,XnX_{1},\dots,X_{n} são independentes e têm distribuição Bernoulli⁢(12)\mathrm{Bernoulli}(\frac{1}{2}). Pela simetria, isso é o mesmo que:

ℙ⁢(X1+⋯+X400⩽185)\mathbb{P}(X_{1}+\dots+X_{400}\leqslant 185)

e, portanto, isso é igual a:

12⋅[1−ℙ⁢(185<X1+⋯+X400<215)]\frac{1}{2}\cdot\Big{[}1-\mathbb{P}(185<X_{1}+\dots+X_{400}<215)\Big{]}

Dado que μ=12\mu=\frac{1}{2} e σ=12\sigma=\frac{1}{2}, reescrevemos convenientemente o evento como:

12−12⋅ℙ⁢(−1.5<X1+⋯+X400−400⋅μσ⁢400<1.5)\frac{1}{2}-\frac{1}{2}\cdot\mathbb{P}\Big{(}{-}1.5<\frac{X_{1}+\dots+X_{400}-% 400\cdot\mu}{\sigma\sqrt{400}}<1.5\Big{)}

e, usando o Teorema do Limite Central, aproximamos por:

12−12⁢∫−1.51.512⁢π⁢e−x2/2⁢dx≈0.07\frac{1}{2}-\frac{1}{2}\int_{-1.5}^{1.5}\frac{1}{\sqrt{2\pi}}e^{-x^{2}/2}\,% \mathrm{d}x\approx 0.07

Você não deve tentar calcular esta integral em casa, a única maneira de obter esse valor é consultando uma tabela, veremos mais sobre isso posteriormente. Portanto, a resposta é 0.07, ou 7

Observe que fornecemos apenas uma resposta aproximada com uma figura significativa. Para obter mais precisão do que isso, seriam necessárias considerações mais cuidadosas e seriam o tema de módulos mais avançados.

Refer to caption
Figura 12.2: Função de probabilidade de Sn−n⁢μσ⁢n\smash{\frac{S_{n}-n\mu}{\sigma\sqrt{n}}} para SnS_{n} com distribuições Binom⁢(4,12)\mathrm{Binom}(4,\frac{1}{2}) e Binom⁢(16,12)\mathrm{Binom}(16,\frac{1}{2}) para valores entre −3-3 e 33. A área de cada retângulo é dada pela função de probabilidade. O terceiro gráfico é a função de densidade de uma normal padrão, assim como as linhas pontilhadas. O quarto gráfico representa as frequências relativas de Sn−n⁢μσ⁢n\smash{\frac{S_{n}-n\mu}{\sigma\sqrt{n}}} para SnS_{n} com distribuição Binom⁢(16,12)\mathrm{Binom}(16,\frac{1}{2}), em um experimento real com 200200 amostras.

Também podemos usar as "versões de um lado"do Teorema do Limite Central. Dessa forma, o exemplo anterior fica simplificado:

ℙ⁢(X1+⋯+X400⩾215)\displaystyle\mathbb{P}(X_{1}+\dots+X_{400}\geqslant 215) =ℙ⁢(X1+⋯+X400−400⋅μσ⁢400⩾1.5)\displaystyle=\mathbb{P}\Big{(}\frac{X_{1}+\dots+X_{400}-400\cdot\mu}{\sigma% \sqrt{400}}\geqslant 1.5\Big{)} (12.3)
≈∫1.5+∞12⁢π⁢e−x2/2⁢dx\displaystyle\approx\int_{1.5}^{+\infty}\tfrac{1}{\sqrt{2\pi}}e^{-x^{2}/2}\,% \mathrm{d}x (12.4)
≈0.07.\displaystyle\approx 0.07. (12.5)

Se reescrevermos o Teorema do Limite Central como

ℙ⁢(μ+σn⁢a⩽X1+⋯+Xnn⩽μ+σn⁢b)≈∫ab12⁢π⁢e−x2/2⁢dx,\mathbb{P}\Big{(}\mu+\frac{\sigma}{\sqrt{n}}a\leqslant\frac{X_{1}+\dots+X_{n}}% {n}\leqslant\mu+\frac{\sigma}{\sqrt{n}}b\Big{)}\approx\int_{a}^{b}\tfrac{1}{% \sqrt{2\pi}}e^{-x^{2}/2}\,\mathrm{d}x,

obtemos uma boa descrição do comportamento estatístico da média observada X1+⋯+Xnn\frac{X_{1}+\dots+X_{n}}{n}. Conforme previsto pela lei das médias, a média observada está concentrada em torno de μ\mu, mas agora podemos dizer algo mais preciso. A média observada flutua como μ+σ⁢1n⁢Z\mu+\sigma\frac{1}{\sqrt{n}}Z, onde ZZ é essa "coisa"descrita por

ℙ⁢(a⩽Z⩽b)=∫ab12⁢π⁢e−x2/2⁢dx.\mathbb{P}(a\leqslant Z\leqslant b)=\int_{a}^{b}\tfrac{1}{\sqrt{2\pi}}e^{-x^{2% }/2}\,\mathrm{d}x.

Variáveis aleatórias descritas em termos de integrais são chamadas de variáveis aleatórias contínuas, que é o tema da próxima seção.