14 Uma única teoria para discretas e contínuas

14.1 Função de distribuição cumulativa

Uma maneira de especificar uma distribuição de probabilidade em $\mathbb{R}$ é dizer o quanto de probabilidade está à esquerda de cada ponto $x$ . Em termos de uma variável aleatória $X$ com a distribuição dada, essa probabilidade é uma função de $x$ .

Definição 14.1.

Seja $X$ uma variável aleatória. A função de distribuição cumulativa de $X$ é a função $F_{X}:\mathbb{R}\to[0,\infty)$ definida por

F_{X}(x)=\mathbb{P}(X\leqslant x)

para todo $x\in\mathbb{R}$ .

Outras probabilidades a partir de $F_{X}$

Agora, observamos que, embora $F_{X}(x)$ seja definido como $\mathbb{P}(X\leqslant x)$ , é possível usar $F_{X}$ para obter outras probabilidades envolvendo $X$ . Fórmulas importantes são

\mathbb{P}(X>x)=1-\mathbb{P}(X\leqslant x)=1-F_{X}(x)

e, para $x<y$ ,

\mathbb{P}(x<X\leqslant y)=\mathbb{P}(X\leqslant y)-\mathbb{P}(X\leqslant x)=F% _{X}(y)-F_{X}(x).

Observe também que

\mathbb{P}(X=x)>0\quad\text{se e somente se}\quad F_{X}\text{ tem um salto em% \leavevmode\nobreak\ $x$}

e, nesse caso, o tamanho do salto é a probabilidade de $X=x$ .

$F_{X}$ determina $\mathbb{P}_{X}$

Proposição 14.2.

Se $X$ e $Y$ são duas variáveis aleatórias com $F_{X}=F_{Y}$ , então $X$ e $Y$ têm a mesma distribuição.

Essa proposição nos diz que a função de distribuição cumulativa realmente codifica a distribuição de uma variável aleatória (no sentido de que, dada a função de distribuição cumulativa, há apenas uma distribuição correspondente a ela).

Já vimos que $F_{X}$ determina $\mathbb{P}_{X}(\{x\})$ para cada $x\in\mathbb{R}$ e $\mathbb{P}_{X}((a,b])$ para todo $a<b\in\mathbb{R}$ .

Faltam-nos as ferramentas necessárias para provar que ela determina $\mathbb{P}_{X}(B)$ para todo $B\in\mathcal{B}$ .

14.2 Casos discretos e contínuos

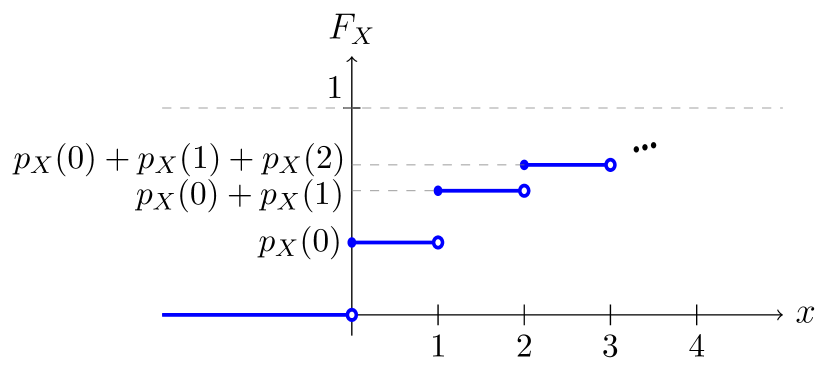
Refer to caption — Figura 14.1: Função de distribuição cumulativa de uma variável aleatória discreta.

Para obter uma primeira ideia de como se parece uma função de distribuição cumulativa, consideremos o caso em que $X$ é discreto e tem suporte discreto contido em $\mathbb{N}_{0}$ , de modo que

\sum_{k=0}^{\infty}\mathbb{P}(X=k)=1.

Em seguida, observe primeiro que $F_{X}(x)=\mathbb{P}(X\leqslant x)=0$ para todos os $x<0$ . A seguir, e para todo $x\in[0,1)$ ,

F_{X}(x)=\mathbb{P}(X\leqslant x)=\mathbb{P}(X<0)+\mathbb{P}(X=0)+\mathbb{P}(0% <X\leqslant x)=0+p_{X}(0)+0=p_{X}(0).

Ao argumentar de maneira semelhante, concluímos que

F_{X}(x)=\begin{cases}0&\text{se }x<0,\\ p_{X}(0)&\text{se }x\in[0,1),\\ p_{X}(0)+p_{X}(1)&\text{se }x\in[1,2),\\ p_{X}(0)+p_{X}(1)+p_{X}(2)&\text{se }x\in[2,3)\\ \cdots\end{cases}

O gráfico de $F_{X}$ se parece com o da Figura 14.1.

Se $X$ for contínuo, então

F_{X}(x)=\mathbb{P}(X\leqslant x)=\mathbb{P}(X\in(-\infty,x])=\int_{-\infty}^{% x}f_{X}(y)\mathrm{d}y.

O teorema fundamental do Cálculo implica então que, nos pontos onde $f_{X}$ é contínuo,

f_{X}(x)=\tfrac{\mathrm{d}}{\mathrm{d}x}F_{X}^{\prime}(x),

ou seja, a função de distribuição cumulativa é diferenciável e sua derivada é a função de densidade de probabilidade. O gráfico de $F_{X}$ se parece com o das Figuras 14.2 e 14.3.

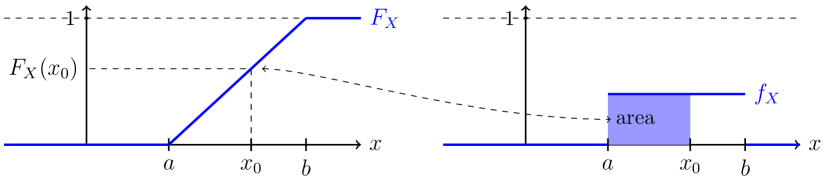
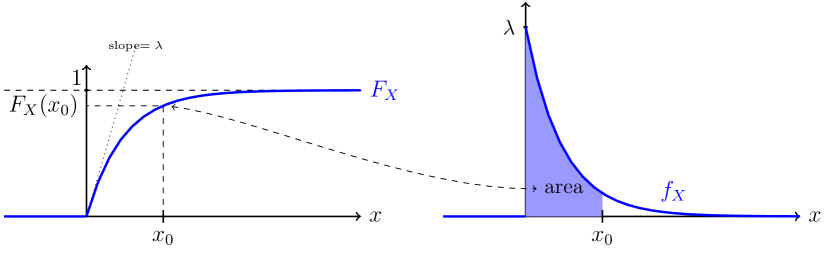
14.3 Esperança e variância

É possível fornecer uma definição unificada de esperança de uma variável aleatória, sem assumir que ela seja discreta ou que tenha uma densidade. Há uma fórmula mágica usando $F_{X}$ que funciona simultaneamente para qualquer tipo de variável aleatória. Não vamos nos preocupar em fornecer tal fórmula, mas é importante ter em mente que a esperança é algo que pode ser definido para qualquer variável aleatória limitada (e, desde que algumas somas ou integrais sejam convergentes, também pode ser definida para variáveis aleatórias ilimitadas). Novamente, dizemos que $X$ é integrável se $\mathbb{E}[X]$ for definido e finito.

Essa definição geral de esperança ainda satisfaz as três propriedades:

•

Unitária: $\mathbb{E}[\mathds{1}_{A}]=\mathbb{P}(A)$ ,
•

Monótona: Se $0\leqslant Z\leqslant X$ para todo $\omega\in\Omega$ , então $0\leqslant\mathbb{E}[Z]\leqslant\mathbb{E}[X]$ ,
•

Linear: $\mathbb{E}[aX+bY]=a\mathbb{E}[X]+b\mathbb{E}[Y]$

desde que $X$ e $Y$ sejam integráveis.

Não provaremos essas propriedades. Claro, não poderíamos possivelmente prová-las, pois nem mesmo fornecemos a definição geral de esperança. Mas mesmo que tivéssemos escrito a fórmula, com as ferramentas atuais não seríamos capazes de provar que a esperança é linear em geral. A ideia da prova é a seguinte: quaisquer variáveis aleatórias $X$ e $Y$ podem ser aproximadas por variáveis aleatórias discretas $X^{\prime}$ e $Y^{\prime}$ e, uma vez que $\mathbb{E}[X^{\prime}+Y^{\prime}]=\mathbb{E}[X^{\prime}]+\mathbb{E}[Y^{\prime}]$ , concluímos que $\mathbb{E}[X+Y]=\mathbb{E}[X]+\mathbb{E}[Y]$ .

Mais uma vez, e $X$ é quadraticamente integrável se $\mathbb{E}[X^{2}]$ for finito, e observe que se $X$ é quadraticamente integrável, então ele é automaticamente integrável (porque $|x|\leqslant 1+x^{2}$ ).

Definição 14.3 (Variância).

A variância de uma variável aleatória quadraticamente integrável $X$ é definida como

\mathrm{Var}(X)=\mathbb{E}[(X-\mathbb{E}[X])^{2}].

Observamos que a desigualdade de Chebyshev é válida para qualquer variável aleatória quadraticamente integrável. De fato, na prova dada na Seção 10.2, usamos apenas as propriedades de esperança mencionadas acima e nada mais.

Definição 14.4 (Covariância).

Também definimos a covariância de duas variáveis aleatórias quadraticamente integráveis como

\mathrm{Cov}(X,Y)=\mathbb{E}[(X-\mathbb{E}[X])(Y-\mathbb{E}[Y])]

e dizemos que elas são não correlacionadas se sua covariância for zero.

Observe que a covariância possui todas as propriedades mencionadas na Seção 9.2. De fato, a prova dessas propriedades usou apenas as três propriedades de esperança mencionadas acima e nada mais. Em particular, o Corolário 9.23 vale em geral, ou seja,

\mathrm{Var}(X_{1}+\dots+X_{n})=\mathrm{Var}(X_{1})+\dots+\mathrm{Var}(X_{n})

desde que $X_{1},\dots,X_{n}$ sejam não correlacionados.

A independência é discutida na próxima seção.